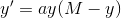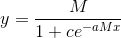Matematik
Integralregning?
Tabellen viser en opgørelse af antal fødedygtige ulvepar i en population af ulve i det centrale Idaho i 1996 og i 2007.
Årstal: 1996 2007
Antal fødedygtige ulvepar: 3 43
I en model for antal fødedygtige ulvepar N som funktion af tiden t (målt i antal år efter 1996) gælder det at:
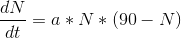
a) Bestem forskriften for N
b) Benyt modellen til at bestemme den øvre grænse for antallet af fødedygtige ulvepar i det centrale Idaho, og benyt modellen til at bestemme det tidspunkt, hvor væksthastigheden for antallet af fødedygtige ulvepar er størst.
Hvordan løser man opgaven? Hvilke værktøjer skal jeg bruge?
- Er næsten sikker på, at jeg skal benytte integralregning, men ved ikke hvordan.
På forhånd tak
Svar #1
04. oktober 2014 af Andersen11 (Slettet)
a) Differentialligningen er den logistiske differentialligning. Man kan her benytte udtrykket for den fuldstændige løsning (slå op i bogen). Man benytter de opgivne datapunkter til at fastlægge konstanterne.
b) Den øvre grænse for N er konstanten 90 i differentialligningen.
Væksthastigheden dN/dt er størst, hvor d2N/dt2 = 0 . Bemærk, at dN/dt er et 2.-gradspolynomium i N.
Svar #3
04. oktober 2014 af Hippocampus (Slettet)
Du skal benytte, at den generelle løsning for differentialligninger af typen
y' = a·y·(M-y)
er givet ved
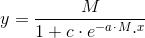
Svar #4
04. oktober 2014 af LeonhardEuler
b) Du kan eventuelt lade N(t) → a for t→∞ og se hvad N(t) går imod.
Svar #5
04. oktober 2014 af saraanderson (Slettet)
#1a) Differentialligningen er den logistiske differentialligning. Man kan her benytte udtrykket for den fuldstændige løsning (slå op i bogen). Man benytter de opgivne datapunkter til at fastlægge konstanterne.
b) Den øvre grænse for N er konstanten 90 i differentialligningen.
Væksthastigheden dN/dt er størst, hvor d2N/dt2 = 0 . Bemærk, at dN/dt er et 2.-gradspolynomium i N.
a) Med konstanterne menes der vel a, som er hældningen?
b) Beregnes væksthastigheden ved at sætte de opgivne data ind? Og hvad står d for helt præcist?
Svar #6
04. oktober 2014 af Heptan
#5
a) Med konstanterne menes der vel a, som er hældningen?
Ja, der menes a, men det er ikke en hældning i dette tilfælde. Derudover er der konstanten c. c står for constant.
b) Hvad står d for?
d står for 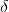 , dvs. delta. Den angiver en lille vækst eller sådan noget, men det ved Andersen11 nok mere om.
, dvs. delta. Den angiver en lille vækst eller sådan noget, men det ved Andersen11 nok mere om.
Det er det samme d som står i differentialligningen fra #0, og eksponenten kommer af, at man differentierer denne.
Væksthastigheden er altså størst når:
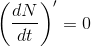
Jeg skal dog ikke gøre mig klog på hans notation...
Svar #7
04. oktober 2014 af Heptan
b) Hvad står d for?
For at undgå forvirring omkring kvadratet på den første afledte:
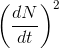
... og udtrykket for den anden afledte, skriver man den anden afledte som:
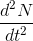
istedet for
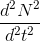 .. eller hvad man nu kan fristes til at skrive.
.. eller hvad man nu kan fristes til at skrive.
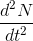 skal læses "(d nummer 2 gange N) delt med (d gange t i anden)
skal læses "(d nummer 2 gange N) delt med (d gange t i anden)
b) Beregnes væksthastigheden ved at sætte de opgivne data ind?
Væksthastigheden for differentialigningen bestemmes ved at differentiere differentialligningen, og "toppunktet" for denne væksthastighed bestemmes ved at løse ligningen:
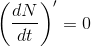
#1
Man benytter de opgivne datapunkter til at fastlægge konstanterne.
Svar #8
04. oktober 2014 af LeonhardEuler
Det er Leibniz's notation 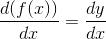 (da y = f(x)), som har sin fordel over for Newtons notation
(da y = f(x)), som har sin fordel over for Newtons notation 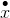
Nu om dage benyttes Lagrange's notation f'(x)
De tre forskellige notationer svarer til hinanden 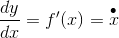
Igen skal det pointeres, at man fandt Leibniz notation mere fordelagtig i datiden (og nu), derfor blev der primært benyttet af Leibniz's notation - med undtagelse af England, hvor Newton stammede fra. Selvfølgelig skulle de engelsk matematikkere støtte Newton's notation ellers ville det være forræderi ... :-)
Fordelen i Leibniz's notation ligger i, at differentialkvoienten bliver skrevet op som en brøk, hvilket man snedigt kan udnytte/misbruge i matematik.
Svar #9
05. oktober 2014 af Andersen11 (Slettet)
Væksthastigheden dN/dt er størst, hvor dens tidsafledede (dN/dt)' er lig med 0. Man kan med fordel benytte differentialligningen til at bestemme, maksimum for væksthastigheden, idet man har
dN/dt = a·N·(90-N) = -a·N2 + 90a·N
Væksthastigheden dN/dt er altså et 2.-gradspolynomium i N, og da koefficienten til N2 er negativ, har polynomiet maksimum i toppunktet, og væksthastigheden er derfor størst mulig, når N = 90/2 = 45 . Tildspunktet for dette kan så findes ud fra den det færdige udtryk for N(t) .
Skriv et svar til: Integralregning?
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.