Matematik

Dobbeltpunkter for vektorfunktioner

11. februar 2023 af tangent - Niveau: A-niveau

Hej,

jeg har fået denne opgave, men er i tvivl om hvordan det skal løses. Der står at man skal bestemme den anden værdi af t, der giver samme punkt på kurven. Jeg forstår det som om, at man skal finde t_2. Derfor har jeg sat koordinatfunktionen x(t)=0 og har derefter løst for t, hvorved jeg få t=0. Herefter indsætter jeg t=0 i koordinatfunktionen y(t), hvorved jeg får y(0)=-4. Det giver ikke mening, for så vidt jeg forstår, burde det give koordinatsættet på dobbeltpunktet, som i øvrigt fås til (0,5.87).

Kan I hjælpe med opgaven?

Tak på forhånd

Vedhæftet fil: Skærmbillede 2023-02-11 kl. 13.38.29.png

Brugbart svar (0)

Svar #1
11. februar 2023 af ringstedLC

Brugbart svar (0)

Svar #2
11. februar 2023 af jl9

$r(\pi)=(sin(\pi),\pi^2-4)=(0,\pi^2-4)$

Prøv hvad det giver med minus Pi

Brugbart svar (0)

Svar #3
11. februar 2023 af ringstedLC

$\begin{align*} y(t)={t_2}^2-4 &= {t_1}^2-4 \\ |t_2| &= \sqrt{\pi^2} \end{align*}$

Svar #4
11. februar 2023 af tangent

#2
$r(\pi)=(sin(\pi),\pi^2-4)=(0,\pi^2-4)$

Prøv hvad det giver med minus Pi

Det giver punktet (0.05480367, 5.869604), som ikke er dobbeltpunktet. Dobbeltpunktet fås til (0,5.87) i GeogGebra. Burde r(π) ikke give dobbeltpunktets koordinater, hvis det er den tilhørende t-værdi?

Svar #5
11. februar 2023 af tangent

#3
b.

$\begin{align*} y(t)={t_2}^2-4 &= {t_1}^2-4 \\ |t_2| &= \sqrt{\pi^2} \end{align*}$

Jeg forstår ikke rigtigt baggrunden for denne beregning. Kan du måske forklare det?

Jeg har nemlig prøvet at indsætte de funden værdier i din formel, men jeg får to forskellige værdier:

t_2^2-4=5,869604

t_1^2-4=-3

Brugbart svar (0)

Svar #6
11. februar 2023 af jl9

#4 Få lige styr på hvad sin(pi) giver

Brugbart svar (0)

Svar #7
11. februar 2023 af ringstedLC

#5: Dobbeltpunktet (-punkterne) har en y-værdi = y(t). Den ene af løsningerne giver t₂ = t₁ som forkastes.

$\begin{align*} {t_1}^2-4 &= -3\Rightarrow t_1=\pm1\;{\color{Red} \neq }\;\pi \end{align*}$

Regn i eksakte værdier istedet for π²med 6 decimaler.

Svar #8
12. februar 2023 af tangent

#7
#5: Dobbeltpunktet (-punkterne) har en y-værdi = y(t). Den ene af løsningerne giver t₂ = t₁ som forkastes.

$\begin{align*} {t_1}^2-4 &= -3\Rightarrow t_1=\pm1\;{\color{Red} \neq }\;\pi \end{align*}$

Regn i eksakte værdier istedet for π²med 6 decimaler.

Problemet er bare, at jeg ikke får en løsning der giver t_2=t_1 og som dermed kan forkastes.

I starten løser jeg ligningen sin(t)=0 for t. Som giver t=0. Herefter sætter jeg t=0 i koordinatfunktionen y(t), hvorved jeg får -4.

Når jeg sætter y(t) koordinatfunktionen lig med 5,87 og løser for t, får jeg ±π. og så ved jeg ikke hvad jeg skal stille op med resultatet... Skal jeg sætte resultatet i koordinatfunktionen x(t)?

Svar #9
12. februar 2023 af tangent

#6 #4 Få lige styr på hvad sin(pi) giver

sin(pi)=0,05480367 på WordMat, selvom det burde give 0. Måske er det her det hele går galt.

Brugbart svar (0)

Svar #10
13. februar 2023 af ringstedLC

#8

I starten løser jeg ligningen sin(t)=0 for t. Som giver t=0. Herefter sætter jeg t=0 i koordinatfunktionen y(t), hvorved jeg får -4.

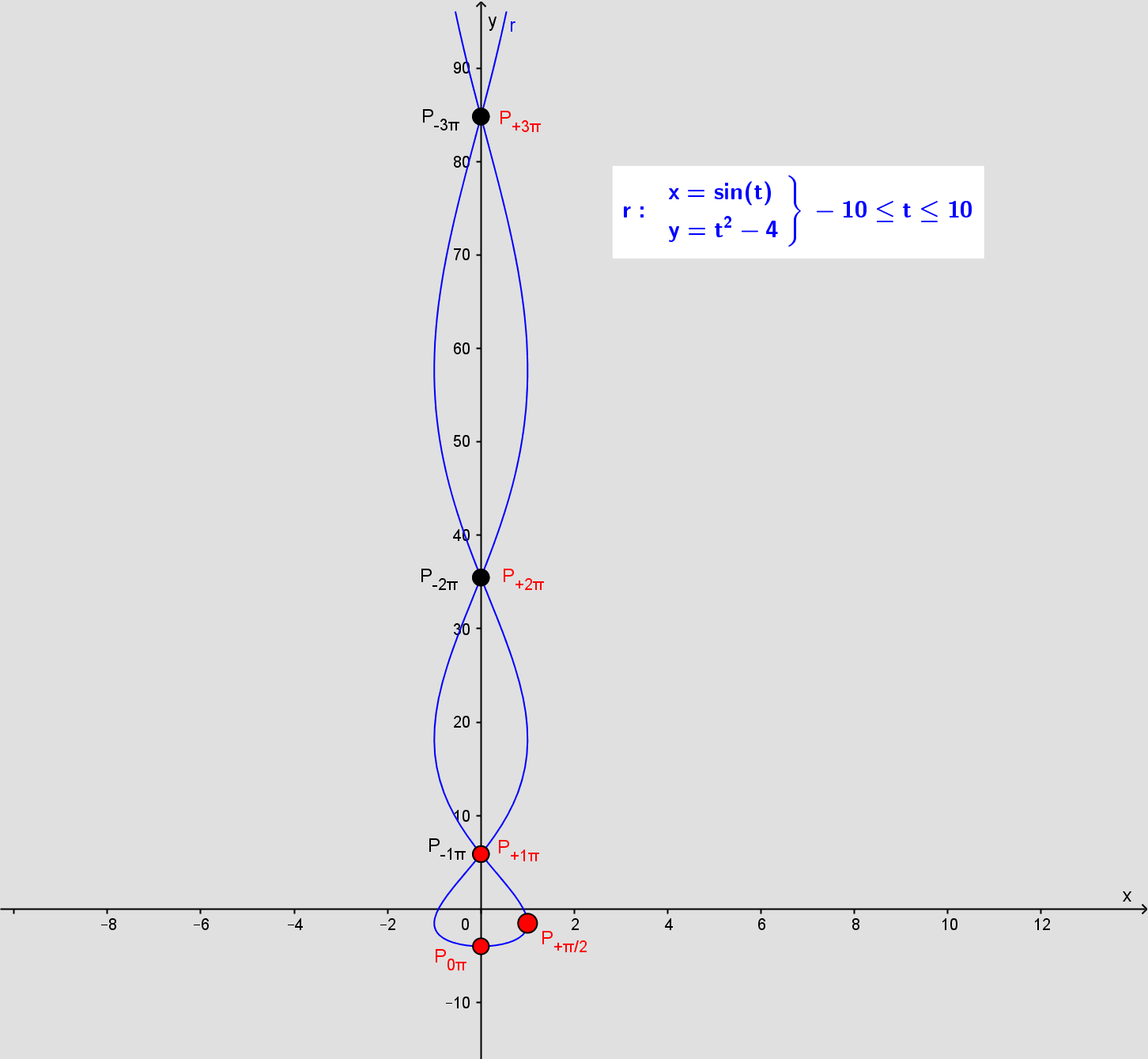
I a. har du tegnet kurven. Se at alle dobbeltpunkterne har x-koordinaten "0".

Det oplyses, at t = π, så det giver ingen mening hverken at løse ligningen eller at indsætte t = 0 i y(t).

Antal dobbeltpunkter:

$\begin{align*} \sin(\pi) &= 0 &&\;\;\;,\; -10\leq &&\ t &&\leq 10 \\ \sin(n\,\pi) &= 0\;,\;n\in\mathbb{Z} &&\Rightarrow -10\leq && n\,\pi &&\leq 10 \\ &&&\quad\;-\tfrac{10}{\pi}\leq &&\ n &&\leq \;\tfrac{10}{\pi} \\ &&&\quad\;\;\,-3\leq &&\ n &&\leq \;\;3 \end{align*}$

Det vil sige, at der er tre dobbeltpunkter i det definerede interval.

Brugbart svar (0)

Svar #11
13. februar 2023 af ringstedLC

$\begin{align*} P_{n\,\pi}=P_{-n\,\pi}&:\binom{0}{(n\,\pi)^2-4} &&=\binom{0}{(-n\,\pi)^2-4}\;,\;t=n\,\pi\;,\;-3\leq n\leq 3 \\ P_{\pi}=P_{-\pi}&:\binom{0}{\pi^2-4} &&=\binom{0}{(-\pi)^2-4} \end{align*}$

Vedhæftet fil:_0.png

Brugbart svar (0)

Svar #12
13. februar 2023 af ringstedLC

#9: Det er selvfølgelig ikke rigtigt. Men det er det, der sker, hvis man bruger afrundede værdier:

$\begin{align*} \sin(\pi)&\;{\color{Red} \neq }\;\sin( 3.14159293)&&=0.05480367 \\\sin(\pi) &= \sin(3.14159265...)&&=0 \end{align*}$

eller skriver forkert af fra lommeregneren. Brug din CAS/lommeregner intelligent, WordMat har en "π-knap".

Men det virker også som om, at du ikke helt har forstået, at det er den anden t-værdi -, og ikke r(π) (dobbeltpunktet), du skal bestemme.

De to punkter, der danner dobbeltpunktet, har samme y(t):

$\begin{align*} y(t)={t_2}^2-4 &= {t_1}^2-4 \\ {t_2}^2 &= \pi^2\;,\;t_1=\pi \end{align*}$ .

Det er en 2. gradsligning med to løsninger, - ellers var det jo ikke et dobbeltpunkt. Den ene er selvfølgelig π, den anden er -π som du også skriver sidst i #8.

Skriv et svar til: Dobbeltpunkter for vektorfunktioner

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.