Side 2 - Andengradsligning - Matematik

Brugbart svar (0)

Svar #21
06. marts 2015 af mathon

Du skal ikke beregne d
men bruge 0-reglen i
ligningen
(x - 4)·(x + 4) = 0

Svar #22
06. marts 2015 af piabing (Slettet)

okay men hvad er formen {r1,r2} helt præcist?

Svar #23
06. marts 2015 af piabing (Slettet)

og hvis ligningen er

-2x^2-2x=0

så løsningen:

-6x=0

ikke?

Brugbart svar (0)

Svar #24
06. marts 2015 af Andersen11 (Slettet)

#22

Der er ingen grund til at bruge lommeregner med disse simple tal.

d = b² - 4·a·c = 0² - 4·(-2)·32 = 8·32 = 2³·2⁵ = 2⁸ = 16² .

Men det simpleste er jo at bruge nulreglen på den faktoriserede ligning.

Brugbart svar (0)

Svar #25
06. marts 2015 af Andersen11 (Slettet)

#23

Den ligning skrives faktoriseret som

-2x·(x + 1) = 0

Benyt nu nulreglen.

Brugbart svar (0)

Svar #26
06. marts 2015 af mathon

#21 fortsat:

Du skal ikke beregne d
men bruge 0-reglen i
ligningen
(x - 4)·(x + 4) = 0

som er meget lettere, når b = 0.

Men selvfølgelig kan ligningen løses med rodformlen, hvis du insisterer:

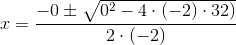
$x=\frac{-0\pm \sqrt{0^2-4\cdot (-2)\cdot 32)}}{2\cdot (-2)}$

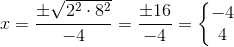
$x=\frac{\pm \sqrt{2^2\cdot 8^2}}{-4}=\frac{\pm 16}{-4}=\left\{\begin{matrix} -4\\ 4 \end{matrix}\right.$

Svar #27
06. marts 2015 af piabing (Slettet)

kan se jeg skal læse meget op. Det er godt fire år siden jeg har haft mat.

Tusind tak for din hjælp

Brugbart svar (0)

Svar #28
06. marts 2015 af mathon

Bemærk de to noget simmplere/lettere løsningsberegninger,
når enten
b eller c er lig med nul.

Brugbart svar (0)

Svar #29
06. marts 2015 af mathon

Generelt:
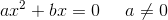
$ax^2+bx=0\; \; \; \; \; a\neq 0$

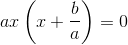
$ax\left (x+\frac{b}{a} \right )=0$

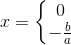
$x=\left\{\begin{matrix} 0\\ -\frac{b}{a} \end{matrix}\right.$

..........

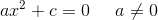
$ax^2+c=0\; \; \; \; \; a\neq 0$

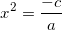$x^2=\frac{-c}{a}$ som kun har reelle løsninger, hvis a og c har modsat fortegn

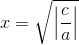
$x=\sqrt{\left | \frac{c}{a} \right |}$

Svar #30
06. marts 2015 af piabing (Slettet)

jeg ved ikke helt om jeg forstår det endnu.

men har lige forsøgt med en ny opgave, hvor jeg brugte nulreglen.

-2x^2-2x=0

-2*x*x-2*x=0

-2x*(x-2)=0

så kan jeg ikke rigtig komme videre.

Brugbart svar (0)

Svar #31
06. marts 2015 af mathon

-2x^2-2x=0

-2*x*x-2*x=0

-2x*(x + 1)=0

Hvis et produkt er lig med nul, skal mindst én af faktorerne være lig med nul.

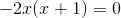
-2x(x+1)=0
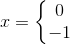
$x=\left\{\begin{matrix} 0\\-1 \end{matrix}\right.$

Svar #32
06. marts 2015 af piabing (Slettet)

hvorfor -1?

Er det fordi -2+1 = -1?

Brugbart svar (0)

Svar #33
06. marts 2015 af mathon

fordi
-1 + 1 = 0

Svar #34
06. marts 2015 af piabing (Slettet)

så tallet -1 har vi fundet, fordi vi skal finde et tal lægger sammen med 1 giver 0?

Forresten.

Kunne du evt. forklare mig lidt om, hvordan man bestemmer definitions- og værdimængde for en funktion. Eks. funktionen: f(x)=(2x+3)2+3

Brugbart svar (0)

Svar #35
06. marts 2015 af Soeffi

#0
Jeg skal løse en andengradsligning.

x^2-7x+12 = 0 ....

For at få en ide om løsningen kan du google x^2-7x+12 som vist. Løsningerne er x værdierne ved grafens skæring med x-aksen.

Vedhæftet fil:andenglign.png

Svar #36
06. marts 2015 af piabing (Slettet)

Kunne du evt. forklare mig lidt om, hvordan man bestemmer definitions- og værdimængde for en funktion. Eks. funktionen: f(x)=(2x+3)2+3

Brugbart svar (0)

Svar #37
06. marts 2015 af Soeffi

#36
Kunne du evt. forklare mig lidt om, hvordan man bestemmer definitions- og værdimængde for en funktion. Eks. funktionen: f(x)=(2x+3)2+3

Funktionen er lineær dvs. x er opløftet i første og ganget med et tal og desuden er et tal lagt til. En sådan funktion er defineret for alle x, dvs. du har lov til at sætte et hvilket som helst tal ind i stedet for x og du kan få alle værdier ud af det. Dermed er definitionsmængde og værdimængde lig med de reelle tal.

Svar #38
06. marts 2015 af piabing (Slettet)

kan definitionsmængde være f.eks.: ]−3,∞[

og værdimængde: ]3,∞[

?

Brugbart svar (0)

Svar #39
06. marts 2015 af Soeffi

#38
kan definitionsmængde være f.eks.: ]−3,∞[

og værdimængde: ]3,∞[

?

Man kan vælge at definitionsmængden skal være ]3,∞[, men så vil værdimængden være (i det lineære tilfælde)

](2·3+3)2+3,∞[ = ]21,∞[.

Man kan ikke vælge begge dele.

Svar #40
06. marts 2015 af piabing (Slettet)

men kan kun vælge mellem disse:

]−∞,∞[
]−3,∞[
[3,∞[
]3,∞[
[−3,∞[