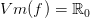Matematik
Surjektiv
Hvorfor nedestående funktion ikke surjektiv:
f: R → R , f(x)=x2
Svar #2
18. januar 2017 af Sneharusha (Slettet)
Jeg forstår ikke helt. Kan du forklare nærmere. :) Er kriereiet ikke bare at alle elementerne i x skal rammer alle elementerne i y en eller flere gange gang. Det bliver der vel også gjort.
Svar #3
18. januar 2017 af fosfor
Hvis f er surjektiv findes x i R så f(x) = -1. Hvis f(x) = -1 løses fås x = +/-i i modstrid med x ∈ R
#3 Ja det er det der er kriteriet, men ikke alle værdier i codomænet antages.
Svar #4
18. januar 2017 af Sneharusha (Slettet)
Tak fordi du vil hjæpe, men jeg forstår det ikke helt. Hvad mener du med at alle codomænet ikke antages.
Svar #5
18. januar 2017 af Sneharusha (Slettet)
Er det fordi (i det jeg har markeret nedefor) y-værdierne ikke bliver ramt af nogle x-værdier?
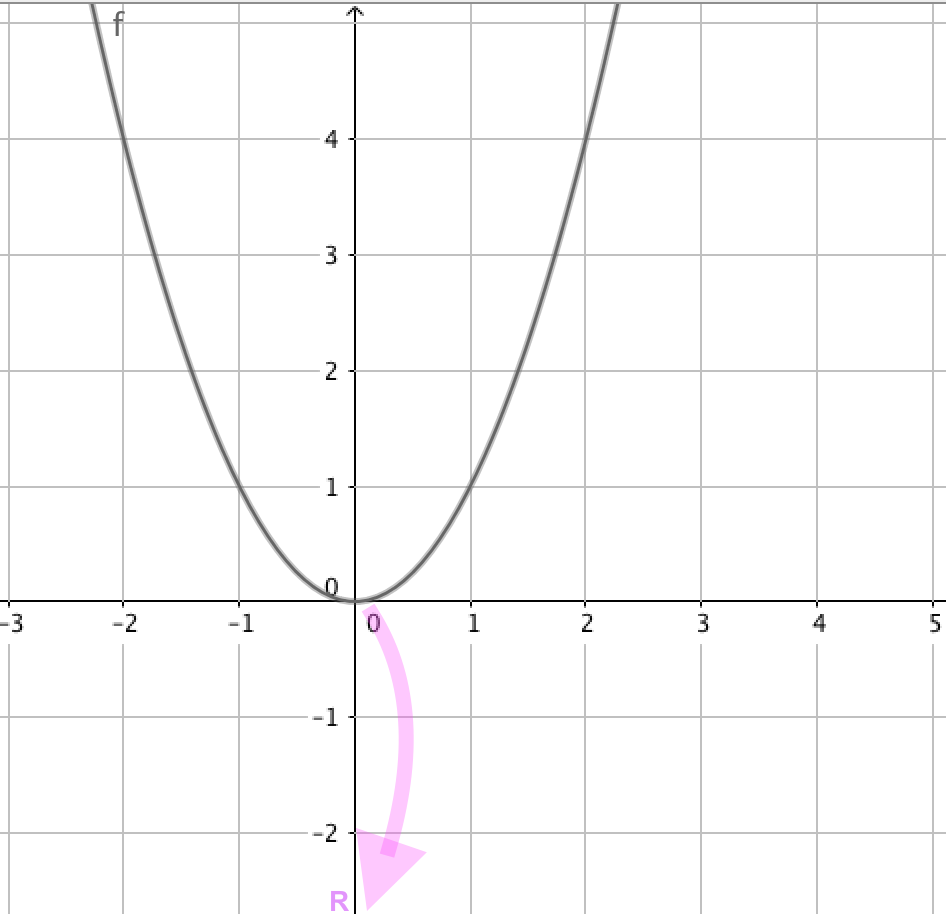
Svar #6
18. januar 2017 af Number42
Ikke R
Hvis R tages som codomæne så er der jo et problem med de negative tal som demonstreret i svar #3 og i #1
Alle tal i Vm(f) skal jo have en x værdi.
Svar #7
18. januar 2017 af AskTheAfghan
Man kan sige, at afbildningen g : A → B er surjektiv, hvis g(A) = B dvs. hvis værdimængden er lig med dispositionsmængden ("codomæne"). For dit tilfælde er f(R) = [0,∞) som ikke er lig med R, men den ligger i R. Afbildningen f : R → [0,∞) er derfor surjektiv, men det er f : R → R ikke.
Svar #8
18. januar 2017 af AskTheAfghan
Ekstra: Det kan arbejdes på en mere stringent måde. Kig hellere på definitionen for surjektivitet. Afbildningen g : A → B siges at være surjektiv, hvis der for ethvert y ∈ B findes et x ∈ A sådan at g(x) = y. Lad nu f : R → R være defineret ved f(x) = x2. Tag y = -1 i definitionen. Kan du finde et x ∈ R sådan at f(x) = -1? Hvis ikke, hvad kan du så sige om det?
Svar #9
20. januar 2017 af Sneharusha (Slettet)
Jeg forstår det virkelig ikke. Jeg vil gerne forstå det, men hver kan jeg tror, at jeg har forstået det, virker det til jeg ikke har forstået det.
Er det ikke fordi, at i forhold til værdimængden i intervallet ]0; ∞[, så har y-værdierne ikke har en tilsvarende x-værdi, at funktionen ikke er surjektiv.
Svar #10
20. januar 2017 af fosfor
Da du skriver f: R → R, så er codomænet R, men f rammer kun [0, ∞[. Surjektivitet er at f rammer hele codomænet.
Svar #11
20. januar 2017 af Sneharusha (Slettet)
Men er det ikkw ofså det jeg skriver:
"... i forhold til værdimængden i intervallet ]0; ∞[, så har y-værdierne ikke har en tilsvarende x-værdi, at funktionen ikke er surjektiv."
Svar #12
20. januar 2017 af Stats
Før at en afbildning f : A → B er surjektiv skal der gælde:
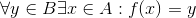
Mvh Dennis Svensson
Svar #13
20. januar 2017 af Stats
#12 fortsat
R er selvfølgelig mængden af alle de reelle tal..
I dit tilfælde har du en afbildning f : R → R hvor f(x) = x2
Altså, for alle y i R eksistere der mindst ét x i R, sådan at f(x) = y...
Nej... For ved y = -2, da kan du ikke finde et x i R, sådan at f(x) = -2
Mvh Dennis Svensson
Svar #14
21. januar 2017 af Sneharusha (Slettet)
Er vi ikke enig om at denne funktion både er injektiv og surjektiv?
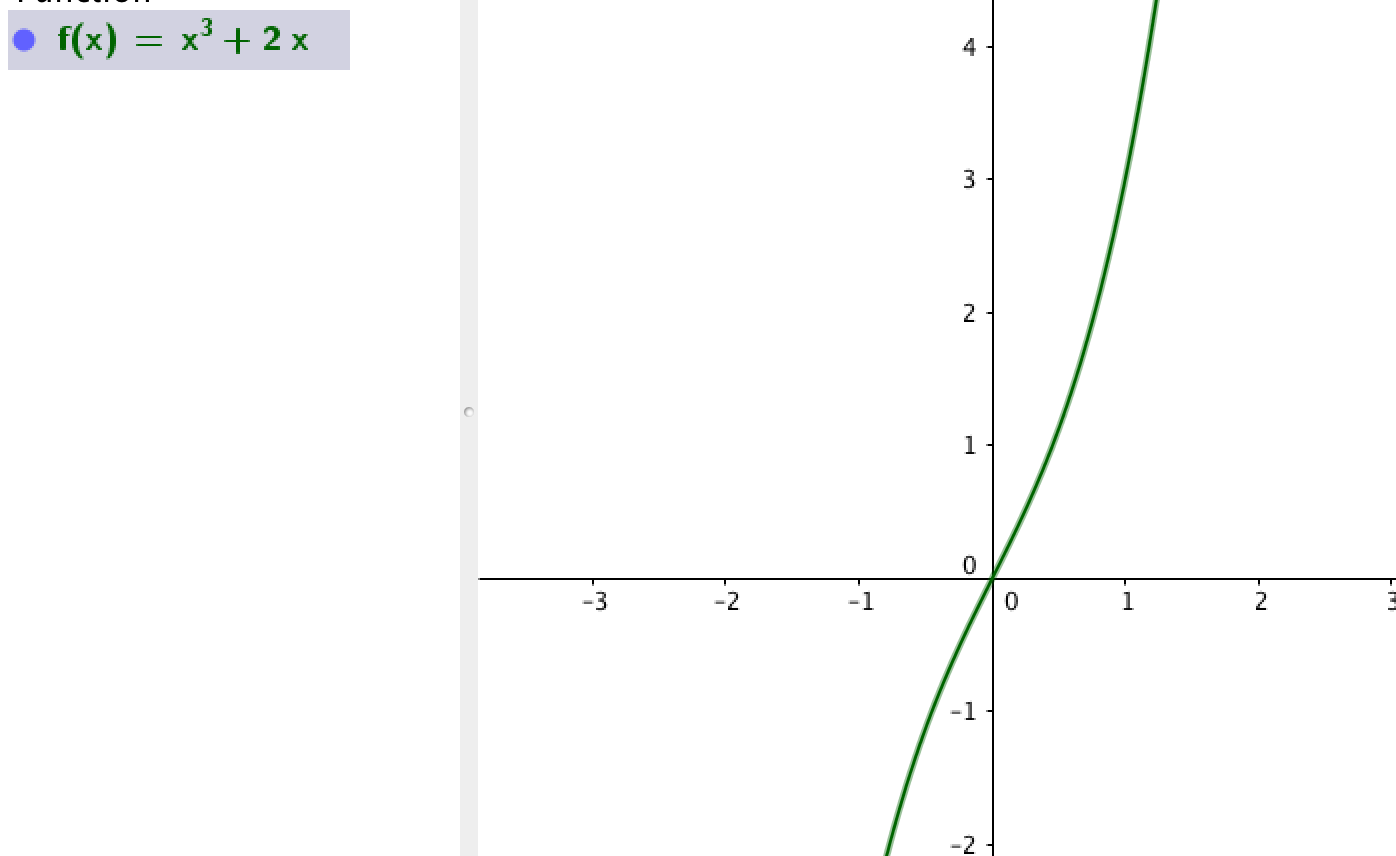
Svar #15
21. januar 2017 af AskTheAfghan
#14 Man kan ikke bare svare på spørgsmålet uden at kende til funktionens definitionsmængde og dispositionsmængde ("codomæne"). Du er også nødt til at forklare hvorfor du synes (bevis?) den er injektiv og surjektiv.
Skriv et svar til: Surjektiv
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.