Matematik

Gammafunktionen

12. april 2017 af sjls - Niveau: Universitet/Videregående

Hej med jer.
Jeg er p.t. i gang med at evaluere værdier i gammafunktionen, og jeg vil gerne finde værdien af 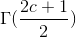$\Gamma(\frac{2c+1}{2})$ , hvor 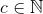$c\in\mathbb{N}$ . Jeg har fundet:

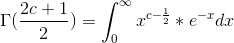
$\Gamma(\frac{2c+1}{2})=\int_{0}^{\infty}x^{c-\frac{1}{2}}*e^{-x}dx$

hvoraf jeg ved substitution af 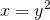x=y^2 får

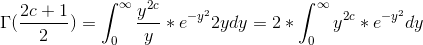
$\Gamma(\frac{2c+1}{2})=\int_{0}^{\infty}\frac{y^{2c}}{y}*e^{-y^2}2ydy=2*\int_{0}^{\infty}y^{2c}*e^{-y^2}dy$

og jeg ved, at 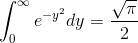$\int_{0}^{\infty}e^{-y^2}dy=\frac{\sqrt{\pi }}{2}$ , men hvordan kommer jeg videre herfra?

Mange tak på forhånd. :-)

Brugbart svar (0)

Svar #1
12. april 2017 af peter lind

Du kan bruge substitutionen t = y² og derefter gentagne gange foretager partiel integration differentiere t^cintegrer e^-t

Der er en fejl i dine resultater. Du får altid et helt tal i eksponenten i y. Det skal du ikke have

Brugbart svar (0)

Svar #2
12. april 2017 af peter lind

glem det sidste

Svar #3
12. april 2017 af sjls

Mange tak for hjælpen. :-)

Jeg har prøvet at gøre som du siger, men jeg ender altså i en cirkelslutning, fordi 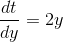$\frac{dt}{dy}=2y$ og

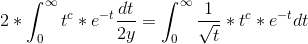$2*\int_{0}^{\infty}t^c*e^{-t}\frac{dt}{2y}=\int_{0}^{\infty}\frac{1}{\sqrt{t}}*t^c*e^{-t}dt$ , og jeg kan ikke lige se, hvordan jeg skal komme ud af denne.

Brugbart svar (0)

Svar #4
12. april 2017 af fosfor

Lad

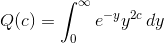
$Q(c)=\int_0^{\infty } e^{-y} y^{2 c} \, dy$

Antag heltallig 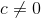$c\neq0$ og integrer første faktor, differentier den anden (partial integration)

$[-e^{-y} y^{2 c}]_0^\infty - \int_0^{\infty } -e^{-y} 2c y^{2 c - 1}dy = 0+2c \int_0^{\infty } e^{-y} y^{2 c - 1}dy = 2c\ Q(c-1/2)$

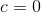Hvis c=0 giver integralet 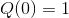Q(0)=1 . Ved ovenstående recursion fås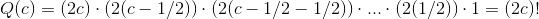 $Q(c)=(2c)\cdot (2(c-1/2))\cdot (2(c-1/2-1/2))\cdot ...\cdot (2(1/2))\cdot 1=(2c)!$

Brugbart svar (0)

Svar #5
12. april 2017 af Therk

Du støder ind i problemer fordi gammafunktionen ikke har en lukket form. Du kan dog stadig godt komme frem til et "ikke-integrale"-resultat for 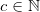$c\in \mathbb N$ , men vi løber her lige en pæn bue uden om evaluering af integralet til det.

Èn værdi af gammafunktion vi dog godt kan udregne er 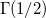, dvs. c = 0.

$\begin{align*} \int_0^\infty x^{-1/2}e^{-x} \, \mathrm dx &= \int_0^\infty 2e^{-u^2}\, \mathrm du \qquad [\text{substituer }u = \sqrt{x}] \\ &= 2 \frac{\sqrt{\pi}}{2} = \sqrt{\pi} \end{align*}$

Til anden lighedstegn er brugt at "u"-integralet kan genkendes som et standard gaussisk integrale (ikke-trivielt integrale, men nemt at se resultatet, når du ved at det er halvdelen af en fordelingsfunktion op til en konstant).

$\rule{7cm}{0.4pt}$

Når det er kendt, så kan vi komme derhen igen ved at benytte en af gammafunktionens egenskaber, nemlig

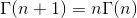$\Gamma(n+1) = n\Gamma(n)$ ,

så ideen er at blive ved med at "trække et argument ud" af gammafunktionen, indtil du er nede på det førstnævnte resultat. Det ser nogenlunde sådan her ud,

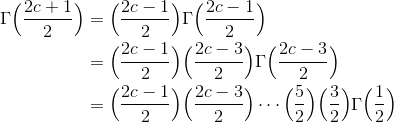
$\begin{align*} \Gamma\Bigl(\frac{2c+1}{2}\Bigr) &= \Bigl(\frac{2c-1}{2}\Bigr)\Gamma\Bigl(\frac{2c-1}{2}\Bigr) \\ &= \Bigl(\frac{2c-1}{2}\Bigr)\Bigl(\frac{2c-3}{2}\Bigr)\Gamma\Bigl(\frac{2c-3}{2}\Bigr) \\ &= \Bigl(\frac{2c-1}{2}\Bigr)\Bigl(\frac{2c-3}{2}\Bigr)\cdots \Bigl(\frac{5}{2}\Bigr)\Bigl(\frac{3}{2}\Bigr)\Gamma\Bigl(\frac{1}{2}\Bigr) \end{align*}$

Du kan nu gange alle nævnerne sammen ved at huske hvor mange brøker du har ganget sammen. Tælleren kan du skrive med fakultet, og 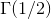fandt vi længere oppe i dette svar.

Jeg har lyst til at færdiggøre argumentationen, men synes du skal have lov til at prøve selv. Prøv at give det et skud og meld tilbage hvad du kommer frem til, eller evt. hvor du går i stå.

Svar #6
13. april 2017 af sjls

Tak for svarene #4 og #5.

Og #5

Jeg har fundet frem til

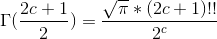$\Gamma({\frac{2c+1}{2}})=\frac{\sqrt{\pi}*(2c+1)!!}{2^c}$ ,

men når jeg skal bruge det i praksis (til at bestemme forskriften for en vilkårlig sandsynlighedstæthedsfunktion til en 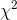$\chi^2$ -fordeling af et ulige antal frihedsgrader), så får jeg et resultat der er en lille smule off. Jeg har brugt

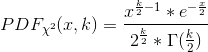
$PDF_{\chi^2}(x,k)=\frac{x^{\frac{k}{2}-1}*e^{-\frac{x}{2}}}{2^{\frac{k}{2}}*\Gamma({\frac{k}{2})}}$

og fået

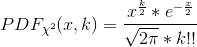
$PDF_{\chi^2}(x,k)=\frac{x^{\frac{k}{2}}*e^{-\frac{x}{2}}}{\sqrt{2\pi}*k!!}$

for k ulige (k=2c+1), hvor k er antal frihedsgrader. Er der en eller anden umiddelbar dum fejl, jeg har lavet? For k lige kunne jeg nemlig sagtens få det til at fungere.

Svar #7
13. april 2017 af sjls

Hov, der skal selvfølgelig stå x^((k/2)-1) i tælleren. Men jeg får stadig et resultat, der ikke er helt korrekt (i al fald ifølge Maple).

Brugbart svar (0)

Svar #8
13. april 2017 af Mathias7878

Respekt for at du kan finde ud af det her sjls, nu hvor der står, at du går i 2g. Fatter ingenting af det her overhovedet ;DD

- - -

Brugbart svar (0)

Svar #9
13. april 2017 af Therk

Det er korrekt, op til en fortegnsfejl. Nu har du ikke vist dine mellemregninger, men du skulle gerne komme frem til at

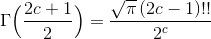
$\Gamma\Bigl(\frac{2c+1}{2}\Bigr) = \frac{\sqrt\pi\,(2c-1)!!}{2^c}$

så du er kommet til at gange med ét led for meget. Dobbeltfakulteten kan du evt. erstatte med

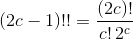
$(2c-1)!! = \frac{(2c)!}{c! \, 2^c}$

men det er semantik; jeg bryder mig bare ikke om dobbeltfakultet.

$\rule{7cm}{0.4pt}$

Hvis du skal bruge resultatet til χ²-fordelingen, så er det nu fint at skrive 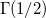. Du kan godt skrive det anderledes, men det bliver ikke pænere.

$\rule{7cm}{0.4pt}$

Må jeg, som en sidebemærkning, nævne at vi helst undgår ordinære brøker (tal over hinanden) i potenser. Da kan det være en fordel at benytte skråstregen som divisionstegn i stedet. Eksempel:

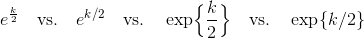
$e^\frac k2 \quad\text{vs.}\quad e^{k/2} \quad \text{vs.} \quad \exp\Bigl\{ \frac k2\Bigr\}\quad \text{vs.}\quad \exp\{k/2\}$

Svar #10
13. april 2017 af sjls

Tusind tak for hjælpen! Det hele fungerer nu! :-)

Tja, jeg syntes bare, det var meget interessant, så jeg har brugt lang tid på at sætte mig ind i det. Men tak :-)

Brugbart svar (0)

Svar #11
13. april 2017 af AskTheAfghan

Må du gerne bruge Legendres fordoblingsformel? Se formlen i (9).

Skriv et svar til: Gammafunktionen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.