Matematik

Funktionfølger

13. juni 2017 af Rossa - Niveau: Universitet/Videregående

Hej Derude.
Jeg prover, at regne en opgave, som lyder:
Lad 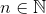$n \in \mathbb{N}$

og 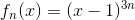$f_n(x)= (x-1)^{3n}$

a. Vis, at 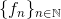$\{ f_n \}_{n \in \mathbb{N}}$ konvergerer punktvis mod en grænsefunktion f på ]0, 2] og find f.

b) Vis, at 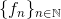$\{ f_n \}_{n \in \mathbb{N}}$ ikke konvergerer uniformt på  ]0, 2].

c) Vis, at 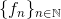$\{ f_n \}_{n \in \mathbb{N}}$ konvergerer uniformt på [a, b], for alle 0 < a < b < 2.

a) Min tanker for opgave a er: For x>2 og x<0 divergerer 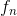f_n .
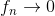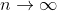For 0< x <2 så vil    $f_n \to 0$    for $n \to \infty$ fordi (x-1) < 1.
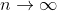
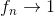For x = 2 har vi (x-1)=1, altså for    $n \to \infty$    $f_n \to 1$ .
Altså 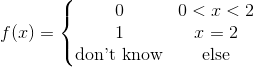$f(x) = \left\{\begin{matrix} 0 & 0 < x < 2 \\ 1 & x=2 \\ \text{don't know} & \text{else} \\ \end{matrix}\right.$

b) På b prøver jeg at bruge følgende teorem, som er på norsk:
La 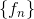$\{ f_n \}$ være en følge av funtsjoner definert på en mengde A, og la 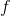være en funksjon som også er defineret på A.
Vi sier at 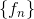$\{ f_n \}$ konvergerer uniformt mot 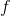på A dersom:

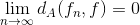
$\lim_{n \to \infty}d_A(f_n, f)=0$

Men det hjælper ikke, og har derfor ikke andre sætning som hjælper.

På opgave c er lost.

Håber, at høre noget nogen som har viljen til at hjælpe.
På forhånd tak

Brugbart svar (0)

Svar #1
13. juni 2017 af peter lind

For x= 0 er f_n(0) = -1 og (-1)³ⁿ er skiftevis -1 og +1. Derfor er den ikke konvergent i 0. Det betyder også at den ikke konvergerer uniformt . [a ; b ] 0<a<b-1 er et lukket interval hvor funktionen er kontinuert

Svar #2
13. juni 2017 af Rossa

a = 0 er ikke med i mængden, ?

Brugbart svar (0)

Svar #3
13. juni 2017 af fosfor

#1 Bortset fra 0 ∉ ]0,2]

2) Du skal vise (jf. theoremet) at d(f, f_n) ikke går mod 0

Bemærk at $2^{-1/3/n}+1$ ∈ ]0,2[ for alle n, så du ved at grænsefunktionen er 0 ved den værdi. Dermed:

d(f, f_n) = sup_x |f(x) - f_n(x)| > |f(2^-1/3/n + 1) - f_n(2^-1/3/n + 1)| = |0 - 1/2| = 1/2

(1/2, 1/2, 1/2, 1/2, 1/2, 1/2, ...) går ikke mod 0.

Brugbart svar (0)

Svar #4
13. juni 2017 af fosfor

c) Grænsefunktionen er 0 på [a, b], så d(f, f_n) er bare ||f_n||_∞

f_n er kontinuert og har et stationært punkt (x=1) hvor værdien er 0. Derfor er

||f_n||_∞ = max(0, lim_x->a |f_n|, lim_x->b |f_n|) = max(0, f_n(a), f_n(b)) som går mod 0 da de tre argumenter går mod 0 hver for sig, da 0<|a-1|<1 og 0<|b-1|<1

Svar #5
13. juni 2017 af Rossa

#3
Jeg kan se, at der er noget som gør mig opmærksom, det vi sige, at det begynde at give mening.
Men, hvad er din f(x) og hvad er din f_n(x)?

Brugbart svar (0)

Svar #6
14. juni 2017 af Number42

Du siger jo selv at fn(x) -> 0 undtagen for x = 2 hvor fn(x) -> 1

funktionen f(x) som fn(x) konvergerer imod er derfor 0 i ]1,2[ og 1 for x =2

f(x) er derfor ikke kontinuert,

En uniformt konvergent følge af kontinuerte funktioner har en kontinuert grænsefunktion

Brugbart svar (0)

Svar #7
14. juni 2017 af Number42

Du er vel klar over at formodentligt hver eneste matamatikbog der omhandler konvergente funtionsfølger beviser:

En uniformt konvergent følge af kontinuerte funktioner har en kontinuert grænsefunktion

Bare nygerrig:

jeg undrer mig: Har du ikke nogen matematikbog for det emne du studerer?

Skriv et svar til: Funktionfølger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.