Matematik

Hjælp til Algebra

27. juni 2017 af Rossa - Niveau: Universitet/Videregående

Hej derude.
Jeg beder om hjælp fordi, det drejer sig om eksamen, og håber, at nogen vil og har lyst til at hjælpe med det emne.
Jeg skal lære nogle egenskaber for Cykliske groupper, som går ud på et spørgsmål i eksamen.

Den cykliske gruppe er defineret som:

A group H is cyclic if H can be generated by a single element, i.e., there is some integer 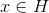$x \in H$ such that:
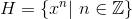$H = \{ x^n | \ n \in \mathbb{Z} \}$ .
Bogen viser en proposition, som jeg har svært med at forstå:

Preposition 5:
Let G be group, let 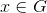$x \in G$ and let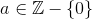 $a \in \mathbb{Z}-\{ 0 \}$
1) if 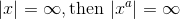$|x| = \infty, \text{then} \ |x^a|= \infty$

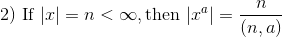
$2) \ \text{If} \ |x| = n <\infty, \text{then} \ |x^a|= \frac{n}{(n,a)}$

3) In particular, 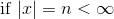   $\text{if} \ |x| = n <\infty$ and  is a positive integer dividing n, then
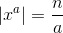
$|x^a| =\frac{n}{a}$
Mine spørgsmål til jer derude:
a) Hvad er 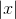|x| ?
Er det orden af 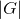|G| , dvs antal af elementer i ?
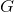Står 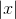|x| for antallet af generators/frembringer eller?

b)
Hvad præsenterer 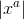|x^a| ?

c)
Det drejer sig om definitionen:
c.1:
Hvis vi har en gruppe G under multiplikation, og dens generator er <1>
Hvordan ser gruppen ud?
Altså
G = (1) ?

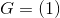c.2
Hvis vi har en gruppe H  under addition, og dens generator er <2>
Vil gruppen være H= (.....,-4,-2,0,2,4,6,...) eller H= (2,4,6,8,...)?

Hvis vi har en gruppe S under MULTIPLIKATION, og dens generator er <2>
Vil gruppen være    S= (2,4,8,16)?

På forhånd tak

.

Brugbart svar (0)

Svar #1
27. juni 2017 af AskTheAfghan

Lad n være et naturligt tal, og lad a være et heltal. Definér restklassen [a]_n af a modulo n ved [a]_n := {a, a ± n, a ± 2n, ...}. Lad Z/nZ betegne mængden af alle restklasser modulo n, og lad (Z/nZ)^× betegne mængden af alle multiplikative inverser i Z/nZ. Bemærk at (Z/nZ)^× er en abelsk gruppe under multiplikativ.

Se eksempelvis på mængden G := (Z/5Z)^×. Her er G = {[1]₅, ..., [4]₅}. Tag et element i G, lad os sige [2]₅. Men [2]₅ = {..., -8, -3, 2, 7, 12, ...}, og da |[2]₅| = ∞, siger Proposition 5, at |[2^b]₅| = ∞ for alle heltal b ≠ 0. Bemærk at [2]₅ er en generator af G (hvorfor?).

Svar #2
27. juni 2017 af Rossa

Du gør teoremen mere abstrakt end det er, nu er jeg helt lost

Brugbart svar (1)

Svar #3
27. juni 2017 af janhaa

x er generator

|x| er orden til generator

ja, |G| er antall elementer til G, gruppas orden.

|x^a|=e

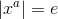
e : identity element.

c1)

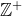
$\mathbb{Z^+}$

c2)

$\mathbb{Z}_3$

Svar #4
27. juni 2017 af Rossa

Mange tak for hjælpen

Brugbart svar (0)

Svar #5
29. juni 2017 af AskTheAfghan

#2 Den første paragraf i #1 er noget man lærer i begyndelsen af abstrakt algebra kursus. Den anden paragraf er et eksempel på, hvordan man arbejder med Proposition 5 og svarer indirekte på dine andre spørgsmål. Når du skriver "Proposition 5", kan jeg se, du bruger Foote's Abstract Algebra. For at læse om den første paragraf, kan du selv tjekke afsnit 0.3 i bogen (s. 8 - 11, 3. udgave). Du skal være opmærksom på, at svaret i #3 ikke er helt korrekt. Trækker mig tilbage.

Skriv et svar til: Hjælp til Algebra

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.