Matematik

vis at f(t) er en løsning

27. februar 2015 af rexden1 - Niveau: Universitet/Videregående

Hejsa,

Jeg forsøger at vise at 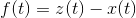f(t) = z(t)-x(t) er en løsning i:

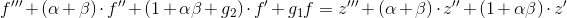
$f'''+(\alpha+\beta)\cdot f''+(1+\alpha \beta +g_2 )\cdot f'+g_1f=z'''+(\alpha + \beta)\cdot z'' + (1+\alpha \beta)\cdot z'$

Jeg finder selvfølgelig alle de nødvendige aflledet af 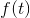f(t) og indsætter i ligningen for at se om de giver højresiden. Problemet er at jeg får en masse led hvori 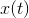x(t) indgår på venstre siden og altså ikke også på højresiden.

Der er endvidere opgivet at 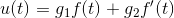u(t) = g_1f(t) +g_2f'(t)

Er der en som har en ide til hvad jeg kan gøre ?

Brugbart svar (0)

Svar #1
27. februar 2015 af Andersen11 (Slettet)

Prøv at formulere hele opgaven. Hvad har u(t) med resten at gøre?

Svar #2
27. februar 2015 af rexden1

Det er nok nemmere at vedhæfte opgaven.

Det drejer sig om opgave 1.3 - U(t) må være en given påvirkning til modellen.

Vedhæftet fil:MiniProjekt1 (3).pdf

Brugbart svar (0)

Svar #3
27. februar 2015 af Andersen11 (Slettet)

Så ved man jo, at

x''' + (α+β)x'' + (1+αβ)x' = u = g₁·f(t) + g₂·f'(t) .

Dermed er, med f(t) = z(t) - x(t)

f''' + (α+β)f'' + (1+αβ+g₂)f' + g₁f = z''' + (α+β)z'' + (1+αβ)z' - x''' - (α+β)x'' - (1+αβ)x' + u(t)

= z''' + (α+β)z'' + (1+αβ)z' - u(t) + u(t)

= z''' + (α+β)z'' + (1+αβ)z'

Svar #4
27. februar 2015 af rexden1

3#:

Der er umiddelbart 2 ting jeg har svært ved at forstå - hvordan kan du udlede at:

x''' + (α+β)x'' + (1+αβ)x' = u = g1·f(t) + g2·f'(t)

og i det sidste lighedstegn, hvordan er venstre og højresiden lig hinanden når der i venstre siden indgår g2 og g1 led ?

Brugbart svar (1)

Svar #5
27. februar 2015 af Andersen11 (Slettet)

I opg 1.2 viser man, at ligning (3) gælder, dvs.

x''' + (α+β)x'' + (1+αβ)x' = u

og i opg 1.3 definerer man

u = g₁·f(t) + g₂·f'(t) ,

hvor

f(t) = z(t) - x(t) .

Derfor har man

f''' + (α+β)f'' + (1+αβ+g₂)f' + g₁f = f''' + (α+β)f'' + (1+αβ)·f' + g₂f' + g₁f

= f''' + (α+β)f'' + (1+αβ)·f' + u(t)

= z''' - x''' + (α+β)(z'' - x'') + (1+αβ)·(z' - x') + u(t)

= z''' + (α+β)z'' + (1+αβ)z' - x''' - (α+β)x'' - (1+αβ)x' + u(t)

= z''' + (α+β)z'' + (1+αβ)z' - u(t) + u(t)

= z''' + (α+β)z'' + (1+αβ)z'

Svar #6
27. februar 2015 af rexden1

okay, ja jeg havde åbenbart glemt hvad jeg havde lavet i opgave 1.2, men så giver det jo megt god mening.

Mange tak for hjælpen

Skriv et svar til: vis at f(t) er en løsning

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.