Punktvis konvergens af funktionsfølger

02. maj 2016 af SuperManBat - Niveau: Universitet/Videregående

Hej er der nogen der kan hjælpe med Opgave 1 Afstand

Mit forsøg

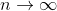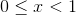
$h_n(x):[0,1] \rightarrow \mathbb{R}\\ x^n \rightarrow 0$ $n \rightarrow \infty$ for $0 \leq x<1$

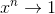
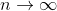$x^n \rightarrow 1$ $n \rightarrow \infty$ for x=1

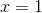
grænsefunktionen h(x) er derfor

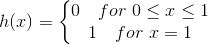
$h(x)=\left\{\begin{matrix} 0 \quad for \ 0\leq x \leq 1 \\ 1 \quad for \ x=1 \end{matrix}\right.$

Denne funktion h(x) er ikke kontinuert på [0,1]

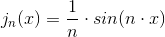
$j_n(x)=\frac{1}{n}\cdot sin(n\cdot x)$

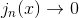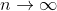
$j_n(x) \rightarrow 0$ for $n \rightarrow\infty$

er grænsefunktionen j lige 0 ?

Er dette rigtigt ?

Hvordan finder grænsefunktionen for 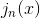j_n(x) , og hvordan beregner jeg afstanden

$d_{[0,1]}(h_n,h)$ og $d_{[0,\pi]}(j_n,j)$

Vedhæftet fil: Screen Shot 2016-05-02 at 21.47.13.png

Brugbart svar (0)

Svar #1
02. maj 2016 af peter lind

Brugbart svar (0)

Svar #2
02. maj 2016 af peter lind

Du har jo fundet de rigtige grænseværdier, så hvorfor spørger du om, hvordan den sidste findes ?

For 0<x<1 har du |f(x)-g(x)| = |xⁿ -0| = xⁿ

for x = 1 har du |f(x)-g(x)| = |1-1| = 0

Den anden. |sin(x)| ≤ 1 og sin(π/2) = 1

Brugbart svar (0)

Svar #3
02. maj 2016 af peter lind

Rettelse til #2 sætningen "Du kan altid som højeste værdi for det få 1/n" bør slettes

Skriv et svar til: Punktvis konvergens af funktionsfølger

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.