Matematik
Taylorrækken for ln(a-x) i 0.
Lad 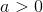 og betragt
og betragt
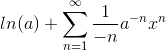
a) Vis, at rækken er Taylorrækken for ln(a-x) i 0.
b) Vis, at rækken konvergerer punktvist i [-a, a[ og uniformt i [-a, b] med -a < b < a.
Nogen der kan hjælpe mig igennem a) og b) er virkeligt forvirret om hvordan jeg beregn Taylorrækken og hvordan jeg viser konvergens/uniformt i b)
Svar #1
22. maj 2016 af peter lind
Du skal finde de afledede for for f(x) = ln(a-x) da a-x > 0 får du x < a
f'(x) = -1/(a-x)
f'(x) = -1/(a-x)2
f''(x) = -2/(a-x)3 o.s.v
Herefter kan du ved induktion vise den generelle formel for f(n)(x) og sætte det ind i formlen for taylorrækken
Svar #2
22. maj 2016 af MieMatematik (Slettet)
Jeg har lidt problemer med induktion kunne du måske vise nogle af trine ?
Svar #3
22. maj 2016 af AskTheAfghan
#2 Der er fortegnsfejl i #1. Man har f '(x) = 1/(x - a), f ''(x) = -1/(x - a)2, og f '''(x) = 2/(x - a)3. Fortsætter man på den måde, "gætter" vi på den generelle formel f(n)(x) = (-1)n-1((n-1)!/(x-a)n+1) for alle n ≥ 1. For at vise, at den passer, skal du vise det ved induktion. Følg resten hvad der står i #1.
Svar #4
22. maj 2016 af peter lind
y = ln(x-a) = ln(u) u= a-x
y' = (dydu)*du/dx = 1/u)*(-1) = -1(a-x)
Der gættes så at f(n)(x)= -n)(a-x)-(n+1)
Antag at det holder for n. Du skal så vise at det også gælder for n+1. Dette gøres ved at differentiere f(n)(x)
Jeg har fået løst opgave a) i denne opgave, men er tilgengæld helt lost opgave b) - er der nogle der kan give et hint til denne opgave?
Svar #6
23. maj 2016 af MacB (Slettet)
Jeg sidder simpelthen fast i den del, hvor man skal differentiere f^(n)(x), for at vise at gættet gælder for n+1 også. Er der nogen der har mulighed for at vise deres metode til dette? :)
Svar #7
23. maj 2016 af peter lind
Det er jo ellers gjort i #4 for n =1.
f(n)(x)= -n!(a-x)-(n+1)
f(n+1) = f(n)(x)= (-n!(a-x)-(n+1))' = (n+1)*n!(a-x)-(n+2)*(-1) = -(n+1)!(a-x)-(n+2)
Svar #8
23. maj 2016 af VandalS
Som bonus information kan I måske bruge at summen ifølge forholdstesten er absolut konvergent når 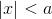 , idet
, idet 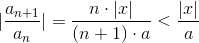 . For
. For 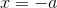 er rækken en aftagende alternerende række og er derfor konvergent ifølge Leibniz' kriterium. Med disse overvejelser vil jeg tro (har ikke tjekket) at I kan benytte sædvanlige
er rækken en aftagende alternerende række og er derfor konvergent ifølge Leibniz' kriterium. Med disse overvejelser vil jeg tro (har ikke tjekket) at I kan benytte sædvanlige 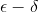 argumenter til at fastslå punktvis/uniform konvergens.
argumenter til at fastslå punktvis/uniform konvergens.
Svar #9
23. maj 2016 af MacB (Slettet)
Det er nok bare fordi jeg ikke kan få det til at gå op i sidste ende, når man skal sætte f^(n)(x)=n!*(a-x)^-(n+1) ind i den genrelle taylorrække og få det ønskede. Sætter i a=0 her? fordi det er i punktet 0. :)
Svar #11
23. maj 2016 af MacB (Slettet)
Jeg får det bare ikke til at være den ønskede taylorrække. Jeg får det derimod til at være summen af (-a)^(n+1). Det er var ikke det opgaven skulle vise. Hvad er det jeg gør forkert? :)
Svar #12
23. maj 2016 af peter lind
Det er mig der i #4 desværre fik skrevet forkert f(n)(x) = - (n-1)!(x-a)-n.
Svar #14
23. maj 2016 af peter lind
Metoden ændres ikke så beviset kan gennemføres med nogle meget små rettelser
Svar #16
23. maj 2016 af peter lind
.Summen af hvad ? Taylorrækken er angivet i #0 så du kan sammenligne med den til kontrol Det har du da vist også gjort tidligere
Svar #17
24. maj 2016 af AskTheAfghan
b) Hint (uniform konvergens): Bestem Mn, som ikke afhænger af x, således at |-(a-n/n)xn| ≤ Mn, for alle n og alle x. Benyt så Weierstraß' M-test for at konkludere resultatet.
Skriv et svar til: Taylorrækken for ln(a-x) i 0.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.





