Sildeben
Et sildeben i matematik er et udtryk, der knytter sig til linjens ligning og til funktioner. Et sildeben er et nyttigt værktøj til at beregne de hjælpepunkter, man skal bruge for at afbilde en funktion grafisk i et koordinatsystem.
Et sildeben anvendes især i forbindelse med lineære funktioner, men kan også benyttes med andre funktioner. Et sildeben består af to rækker, indeholdende den uafhængige variabel øverst og den afhængige variabel nederst.
Et sildeben er en fordeling af x-værdier (øverst) og de tilhørende beregnede y-værdi eller funktionsværdier (nederst). En x-værdi og den tilhørende y-værdi udgør samlet et koordinatsæt. Når man har fundet et passende antal koordinatsæt, kan man tegne en graf for funktionen.
Eksempel 1
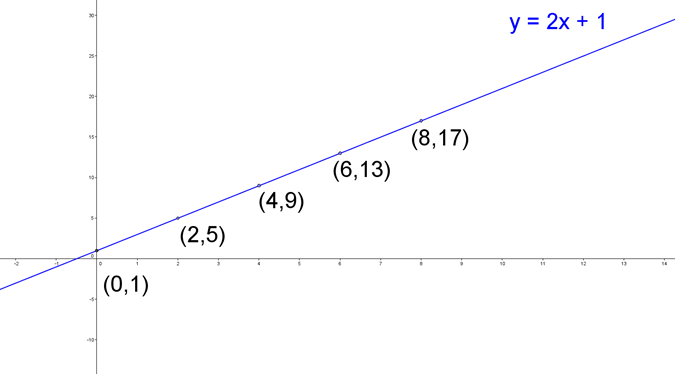
Et sildeben ser således ud:
|
x |
0 |
2 |
4 |
6 |
8 |
|
y = 2x + 1 |
1 |
5 |
9 |
13 |
17 |
I den øverste række indsættes forskellige værdier for den uafhængige variabel x. Nederst er de tilhørende værdier for y udregnet efter linjens ligning: y = 2x + 1. Heraf fremgår det i øvrigt, at skæringen med y-aksen er punktet (0,1) og hældningskoefficienten a = 2
Eksempelvis for x = 4:
Selvom man i realiteten kan tegne en ret linje med kun to punkter, er der en sikkerhed forbundet med at tegne en ret linje med 5 punkter. Disse punkter kan nemmest opstilles i et sildeben og herefter indføres i et koordinatsystem.
Eksempel 2
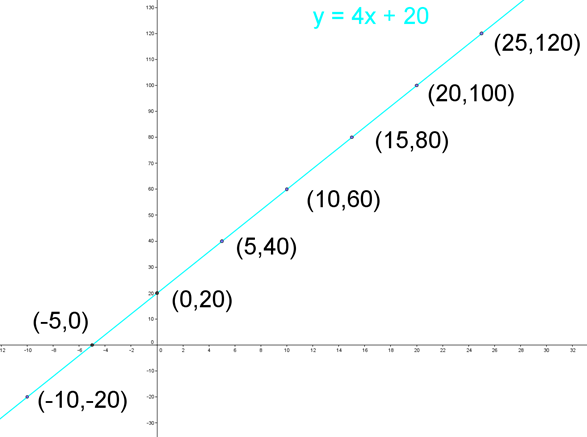
Andre foretrækker at opstille det således, hvor linjens ligning er placeret udenfor sildebenet:
y = 4x + 20
|
x |
-10 |
-5 |
0 |
5 |
10 |
15 |
20 |
25 |
|
y |
-20 |
0 |
20 |
40 |
60 |
80 |
100 |
120 |
Det gør ingen forskel, hvilken metode man vælger. Når man har fundet et passende antal koordinatsæt ved hjælp af ens sildeben, kan grafen indtegnes.
Et sildeben er altså et hjælpeværktøj til funktioner, hvor man på en let-overskuelige måde kan parre en x-værdi og den tilhørende y-værdi. Dermed finder man de koordinatsæt man skal bruge for at kunne tegne funktionen ind i et koordinatsystem. Hvis punkterne alle ligger på en ret linje, er der tale om en lineær funktion også kaldet en lineær sammenhæng mellem to variable.
Sildeben til en parabel
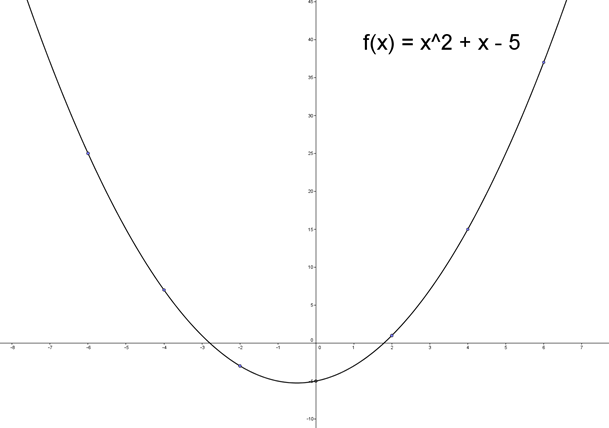
Et sildeben kan også benyttes til at udregne koordinatsæt til et andengradspolynomium. Eksempelvis denne parabel med forskriften:
f(x) = x^2 + x – 5
Funktionsværdier til tilfældigt udvalgte x-værdier er udregnet herunder ved benyttelse af et sildeben.
|
x |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
|
f(x) |
25 |
7 |
-3 |
-5 |
1 |
15 |
37 |
Parablen kan herefter tegnes. Når man indtegner disse punkter på papir og derefter forbinder med en streg, bliver det ikke et perfekt billede. Men man kan alligevel få et godt indtryk af en parabels grafiske udseende med 7 koordinatsæt som i dette eksempel.