Hældningskoefficient

En hældningskoefficient beskriver udseendet på en ret linje, hvor stejl eller flad linjen er. Hældningskoefficient er udtrykt ved konstanten a i linjens ligning og a i en lineær funktion.

Jo større a er desto stejlere er linjen. Hældningskoefficient a kaldes undertiden også for stigningstal, hældningstal eller blot hældning for en graf. Begrebet stigningstal kan dog virke lidt misvisende, da en lineær funktion både kan være stigende/voksende og aftagende. Hældningskoefficient a er tæt knyttet sammen med lineær vækst.

Definitionen på hældningskoefficient er det tal/den koefficient, som en ret linje stiger eller aftager med, når man går én til højre på x-aksen. Hvis x ændrer sig én i positiv retning, hvad er så den tilhørende ændring på y-aksen.

Eksempel på hældningskoefficient

Linjen  har forskriften .

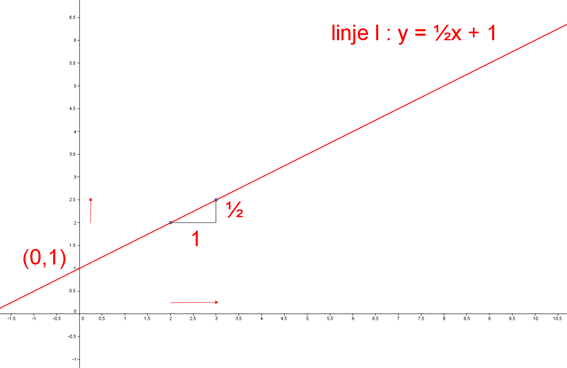
Ud fra definitionen betyder det, at når man bevæger sig 1 til højre på x-aksen, så skal man ½ op på y-aksen for igen at ramme linjen. Det er markeret på figuren, idet en bevægelse på x-aksen fra 2 til 3 ændrer y-koordinatet fra 2 til 2½. Linjens hældningskoefficient a = ½.

Betydningen af a

Der gælder følgende om en hældningskoefficient a, og dermed udseendet af lineære funktioner:

a > 0: Funktionen er voksende, dvs. at når man går fra venstre mod højre bevæger grafen sig op ad.

a = 0: Funktionen er konstant, dvs. at grafen er en vandret linje.

a < 0: Funktionen er aftagende, dvs. at når man går fra venstre mod højre bevæger grafen sig ned ad.

Linjen l er voksende, det ses af at a er positiv (+½).

Linjen g er konstant idet a = 0.

Linjen h er aftagende da a er negativ (-1).

Hældningskoefficient formel

Hældningskoefficienten a er udtrykt ved følgende formel:

Trekanten  er det græske tegn delta, der betyder ændring (forskel på to værdier). Man siger at 'a er lig med delta y over delta x’.

a er lig med ændringen i , divideret med ændringen i .

For at beregne hældningskoefficient a skal man derfor kende to punkters koordinatsæt .

Eksempel

Lad os se på linje h på figuren herunder, hvor punkterne  og  er indsat:

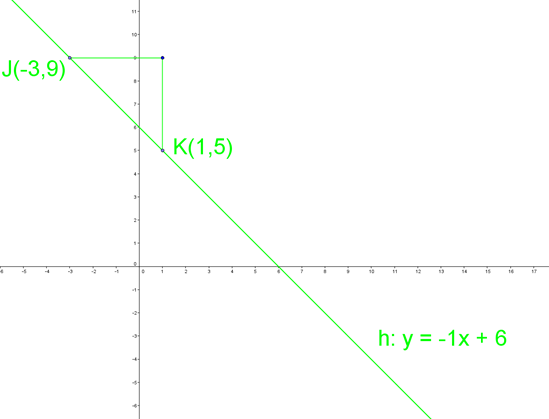
Hældningskoefficienten  indgår som fortegn for x, som det fremgår af linjens ligning for linjen .

For nemheds skyld vil man oftest vælge  til 1, da hældningskoefficienten derved fremgår direkte som .

Har  en anden værdi som i eksemplet med punkterne J og K, skal den tilhørende ændring i  blot indsættes i formlen, for at beregne hældningskoefficienten.

Se endvidere artiklen om lineær sammenhæng for dennes sammenhæng med hældningskoefficient a.

Som opsummering kan det fastslås, at hældningskoefficient a for en lineær funktion beskriver udseendet af den rette linje. Hvis a er positiv, er den rette linje stigende fra venstre mod højre. Hvis a er negativ er den rette linje faldende fra venstre mod højre. Hvis a = 0 er det en vandret linje. 

Hældningskoefficienten beskriver, hvor langt man skal bevæge sig på y-aksen, op eller ned, hvis man bevæger sig 1 til højre på x-aksen.