Matematik
Matematisk analyse
Hej. Jeg sidder med en analyse-opgave, som måske er ret simpel, men jeg har brug for en hjælpende hånd, som kan forklare mig løsningen. Opgaven lyder;
Find summen;
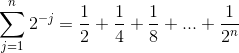
for alle n = 1, 2, 3, 4, ....
Tak på forhånd
Svar #2
08. november 2016 af VandalS
For de første par værdier af 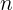 er summen
er summen
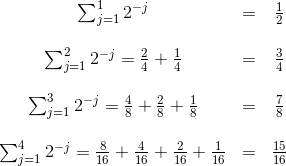
Herfra er det forhåbentligt åbenlyst hvad summen er for et vilkårligt 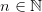 , og for at bevise din formodning kunne du for eksempel føre et induktionsbevis.
, og for at bevise din formodning kunne du for eksempel føre et induktionsbevis.
Svar #3
08. november 2016 af BlackandBlue (Slettet)
Svar #4
08. november 2016 af VandalS
#3
Som du har skrevet det i #0 er summen endelig; selvom 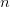 kan være vilkårlig stor kan den ikke være uendelig, så summen er også endelig og har derfor en veldefineret værdi. Med det sagt kan den uendelige sum
kan være vilkårlig stor kan den ikke være uendelig, så summen er også endelig og har derfor en veldefineret værdi. Med det sagt kan den uendelige sum
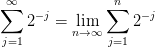
også tilskrives en fornuftig værdi idet afsnitssummen konvergerer.
Svar #5
08. november 2016 af BlackandBlue (Slettet)
Svar #7
08. november 2016 af BlackandBlue (Slettet)
Svar #8
08. november 2016 af VandalS
All right, jeg giver dig min besvarelse så du kan følge min tankegang.
Oplysningen om at 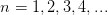 fortæller os, at
fortæller os, at 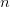 er et naturligt tal.
er et naturligt tal. 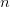 kan derfor være et vilkårligt stort naturligt tal, men ikke være uendelig. Dette betyder at vi kan skrive
kan derfor være et vilkårligt stort naturligt tal, men ikke være uendelig. Dette betyder at vi kan skrive
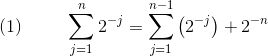
og være sikre på, at det er matematisk velbegrundet, idet begge summer vides at være endelige da 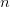 er endelig.
er endelig.
Fra (1) kan du se, at hvis du kender summens værdi for 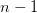 kan du nemt finde værdien for
kan du nemt finde værdien for 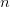 , så summens værdi kan findes rekursivt. Vi udnytter den rekursive sammenhæng til at føre et induktionsbevis, der lader os finde et lukket udtryk for summens værdi. Til dette skal vi bruge tre ting:
, så summens værdi kan findes rekursivt. Vi udnytter den rekursive sammenhæng til at føre et induktionsbevis, der lader os finde et lukket udtryk for summens værdi. Til dette skal vi bruge tre ting:
1. En induktionshypotese, altså vores bud på den lukkede form.
2. En induktionsbase hvori vi ved at induktionshypotesen er sand.
3. Et induktionsskridt der tillader os at konkludere, ud fra vores induktionsbase, at induktionshypotesen er sand for alle 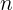 .
.
Ved at skrive summen op for de første par værdier af 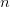 (som i #2) virker det oplagt, at vores hypotese må være at summen har værdien
(som i #2) virker det oplagt, at vores hypotese må være at summen har værdien
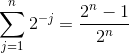 .
.
For 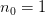 er
er
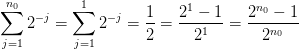
så induktionshypotesen er sand i 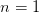 og vi har dermed vores induktionsbase.
og vi har dermed vores induktionsbase.
Til sidst tager vi induktionsskridet. Vi lader derfor 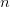 være et vilkårligt naturligt tal og antager, at induktionshypotesen er sand for
være et vilkårligt naturligt tal og antager, at induktionshypotesen er sand for 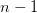 . Vi skal så vise, at induktionshypotesen også er sand for
. Vi skal så vise, at induktionshypotesen også er sand for 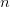 .
.
Ved at bruge formel (1) og vores antagelse har vi, at
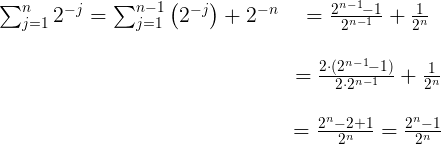
som ønsket. Vi konkluderer, at vores induktionshypotese er sand for alle naturlige tal, altså at
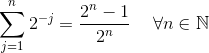 . Q.E.D.
. Q.E.D.
Hvis nogen af teknikkerne eller tankegangen er ny for dig er du velkommen til at stille spørgsmål, så skal jeg vejlede så godt jeg kan.
Svar #9
08. november 2016 af BlackandBlue (Slettet)
Okay, jeg tror det er ved at sidde på plads. Men jeg har lige et sidste spørgsmål; hvor får du ... 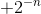 fra i formlen (1) ?
fra i formlen (1) ?
Skriv et svar til: Matematisk analyse
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.








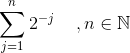
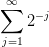 ?
?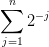
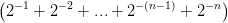 og
og