Lige nu 490 online.

Persondatapolitik

Studieportalen.dk › Kompendier › Matematik › Matematik formelsamling › Procentregning › Procentvis afvigelse

Procentvis afvigelse

Procentvis afvigelse er tæt forbundet med en procentvis ændring. Procentvis afvigelse er et begreb, der især knytter sig til de naturvidenskabelige fag, eksempelvis fysik og kemi, hvor man opererer med tabelværdier. Men det kan også sagtens være matematiske størrelser eller resultater.

Når man beregner et resultat, kan man undersøge, hvor tæt en målt værdi er på tabelværdien. I så fald taler man om afvigelse i procent mellem tabelværdi og den målte værdi.

En procentvis afvigelse er en sammenligning, der beskriver den afstand eller værdi, der er til det, man havde forventet som resultat. Når man dividerer afvigelsen med tabelværdien og ganger med $100 \%$ , finder man en procentvis afvigelse.

Afvigelse kan både være positiv og negativ, fortegnet er med til at afsløre til hvilken side afvigelsen er.

Det er især afgørende med fortegn, hvis man laver mange observationer. I det tilfælde vil man finde ud af, om målingerne konsekvent har en enten positiv eller negativ afvigelse. Når der er tale om en enkelt observation, er procentafvigelse ofte udtrykt numerisk/absolut.

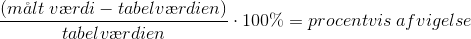
$\frac {(m\aa lt \; v\ae rdi - tabelv\ae rdien)}{tabelv\ae rdien} \cdot 100 \% = procentvis \; afvigelse$

Eksempel 1

Densiteten af en gas er målt til 4,13 kg/m^3 .

Ved opslag er tabelværdien for gassen: 4,28 kg/m^3 .

Hvad er den procentvise afvigelse fra tabelværdien?

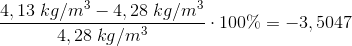
$\frac{4,13 \; kg/m^3 - 4,28 \; kg/m^3}{4,28 \; kg/m^3} \cdot 100 \% = -3,5047 %$

Procentafvigelse for gassens målte densitet i forhold til den faktiske tabelværdi er udtrykt numerisk/absolut = $3,50 \%$ . Da fortegnet er minus viser resultatet at den målte densitet er 3,50 % under den faktiske tabelværdi.

Eksempel 2

I et andet forsøg er tyngdeaccelerationen målt til 9,94 m/s^2 .

Ved opslag er tabelværdien for tyngdeaccelerationen: 9,82 m/s^2 .

Hvad er den procentvise afvigelse fra tabelværdien?

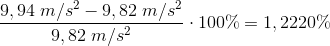
$\frac{9,94 \; m/s^2 - 9,82 \; m/s^2}{9,82 \; m/s^2} \cdot 100 \% = 1,2220 \%$

I forsøget med tyngdeaccelerationen er der en procentafvigelse på $1,22 \%$ i forhold til tabelværdien. Da fortegnet er plus viser dette resultat at den målte tyngdeacceleration er større end den faktiske tabelværdi.

Eksempel 3

Det sidste eksempel handler om Socialdemokratiets tilslutning ved Kommunalvalget 2013 . Valgresultatet fungerer som tabelværdien, og meningsmålingerne fungerer som måleresultater.

Socialdemokratiet fik $29,5 \%$ af alle de afgivne stemmer på landsplan ved Kommunalvalget 2013 .

En meningsmåling (måling viste, at de ville få $24,3 \%$ af stemmerne.

En anden (måling ) viste, at de ville få $22,6 \%$ af stemmerne.

Lad os se på den procentvise afvigelse for de to målinger i forhold til det faktiske valgresultat.

Måling $1: \frac{24,3 \% - 29,5 \%}{29,5 \%} \cdot 100 \% = -17,63 \%$

Måling $2: \frac{22,6 \% - 29,5 \%}{29,5 \%} \cdot 100 \% = -23,39 \%$

Den procentvise afvigelse for Socialdemokratiets valgresultat og de to meningsmålinger er betydelig.

Den procentvise afvigelse er for måling $1 = -17,63 \%$ , for måling $2 = -23,39 \%$ .

Sammenfattende er de to målinger gennemsnitligt $20 \%$ under det faktiske valgresultat, da fortegnet er minus når afvigelsen udregnes.

Det er afgørende, at man dividerer med det, man måler afvigelsen fra (eksempelvis tabelværdien eller det faktisk valgresultat), når man udregner en procentvis afvigelse.

Seneste indlæg
9: Hvad kan man perspektiver med li... (0)
9: Hjælp til at snakke tysk (1)
9: Hævn og tilgivelse religion (2)
A: Syre-base (0)
B: Måling af halveringstid (0)

Populære indlæg
9: Hvad kan man perspektiver med li... (0)
9: Hjælp til at snakke tysk (1)
9: Analyse af "One-night stand... (1)
9: Analyse af Dallas skrevet af Jes... (3)
B: Måling af halveringstid - forsøg (16)

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se