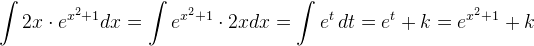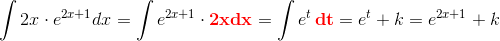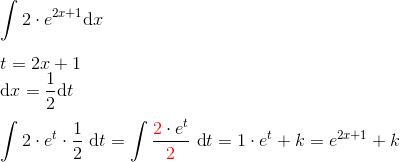Matematik

integrere ved substitution

29. januar 2015 af kasper28 (Slettet) - Niveau: A-niveau

nogen der kan hjælpe med disse 3 opgaver, (vedhæftede) samt give mig en forklaring, er klar over jeg skal skille dem ad, men hvad foregår der så? :) det jeg får passer ikke sammen med det resultat min lommeregner spytter ud.. :)

Vedhæftet fil: mat int.jpg

Brugbart svar (0)

Svar #1
29. januar 2015 af Andersen11 (Slettet)

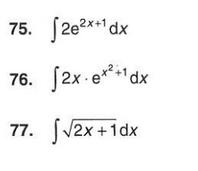
mat int.jpg

75. Benyt substitution t = 2x+1 , dt = 2 dx.

76. Benyt substitution t = x² + 1 , dt = 2x dx

77. Benyt substitution t = 2x+1 , dt = 2 dx

Prøv at vise dine egne resultater.

Brugbart svar (0)

Svar #2
29. januar 2015 af Stats

∫ 2·e^2·x+1 dx = ∫ 2·e^t dx

t = 2x + 1, hvor t er den indre funktion

dt/dx = (2x + 1)' = 2... dt/dx = 2 ⇔1/2 dt = dx
(dt/dx anses normalt ikke som en brøk, men er nyttig i dette tilfælde)

∫ 2·e^t·(1/2) dt = ∫ e^t dt = e^{2x + 1} ....

Anvend den samme metode til resten af opgaverne

- - -

Mvh Dennis Svensson

Brugbart svar (0)

Svar #3
29. januar 2015 af mathon

i 76 har du så

$\int 2x\cdot e^{x^2+1}dx=\int e^{x^2+1}\cdot 2xdx=\int e^{t}\, dt=e^t+k=e^{x^2+1}+k$

Svar #4
29. januar 2015 af kasper28 (Slettet)

lad os lige tage udgangspunkt i den første, er med på hvad der er indre og ydre, og at den blir ændret til t og da (e^t)'=e^t vil den del være det samme. er bare ikke helt med på hvad der sker når 2 tallet forsvinder??

Brugbart svar (0)

Svar #5
29. januar 2015 af Andersen11 (Slettet)

2-tallet "forsvinder" , fordi 2 dx substitueres med dt .

Svar #6
29. januar 2015 af kasper28 (Slettet)

altså sådan her? :)

Vedhæftet fil:matmat.jpg

Brugbart svar (0)

Svar #7
29. januar 2015 af Andersen11 (Slettet)

Man bør afholde sig fra at blande de variable. Man har enten et integral med x, eller et integral med t.

75. Det er forkert at skrive dt = (2x+1)' = 2 . Man har

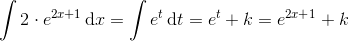
$\int 2\cdot e^{2x+1}\, \textup{d}x=\int e^{t}\, \textup{d}t=e^{t}+k=e^{2x+1}+k$

Tilsvarende kommentarer til 76., der er gennemgået i #3.

Brugbart svar (0)

Svar #8
29. januar 2015 af mathon

75.

$\int 2x\cdot e^{2x+1}dx=\int e^{2x+1}\cdot \mathbf{\color{Red} 2xdx}=\int e^{t}\, \mathbf{\color{Red} dt}=e^t+k=e^{2x+1}+k$

Brugbart svar (0)

Svar #9
29. januar 2015 af Andersen11 (Slettet)

Sådan ser opg 75 ikke ud. Substitutionen er t = 2x+1 , dt = 2 dx . Se #7.

Svar #10
29. januar 2015 af kasper28 (Slettet)

nu begynder det jo at give mening det hele.. tak for hjælpen.. :) hvad siger i til den sidste? tænker mest på hvordan jeg får placeret ½ tegnet...?

Vedhæftet fil:integral.jpg

Brugbart svar (0)

Svar #11
29. januar 2015 af Stats

$\\ \int 2\cdot e^{2x+1} \textrm{d}x\\ \\ t=2x+1\\ \textrm{d}x = \frac{1}{2}\textrm{d}t\\ \\ \int 2\cdot e^t\cdot \frac{1}{2}\ \textrm{d}t = \int \frac{{\color{Red} 2}\cdot e^t}{{\color{Red} 2}}\ \textrm{d}t = 1\cdot e^t +k = e^{2x+1}+k$

- - -

Mvh Dennis Svensson

Svar #12
29. januar 2015 af kasper28 (Slettet)

se lige den vedhæftede var opg 77 jeg tænkte på

Brugbart svar (0)

Svar #13
29. januar 2015 af Andersen11 (Slettet)

#10

Igen skal du lade være med at blande de variable x og t i integralet, som du gør det her. Ellers ser det rigtigt ud. Med substitutionen

t = 2x+1 , dt = 2 dx , dx = (1/2) dt

har man

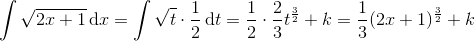
$\int \sqrt{2x+1}\, \textup{d}x= \int \sqrt{t}\cdot \frac{1}{2}\, \textup{d}t=\frac{1}{2}\cdot \frac{2}{3}t^{\frac{3}{2}}+k=\frac{1}{3}(2x+1)^{\frac{3}{2}}+k$

Brugbart svar (0)

Svar #14
29. januar 2015 af Stats

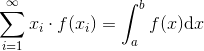
$\sum_{i=1}^{\infty }x_i\cdot f(x_i)=\int_{a}^{b}f(x)\textrm{d}x$

x_i er bredden, og f(x_i) er højden. Dvs bredde gange højde = areal... Integralet er jo en sum, af alle mulige rektangler under grafen. Når der bliver uendeligt mange rektanglerne, da må x_i blive ufattelig lille (ikke målelig), det er den man kalder for dx.. Når en sum går mod uendelig, kan den beskrives ved integraltegnet (uendelige summer)

- - -

Mvh Dennis Svensson

Brugbart svar (1)

Svar #15
29. januar 2015 af Andersen11 (Slettet)

#14

Hvad er det, du forsøger at forklare her? Integralet er ikke en sum af alle mulige rektangler under grafen.

Integralet er en grænseværdi for en middelsum for en funktion f(x) hørende til en intervalinddeling af intervallet [a;b] hvor finheden af intervalinddelingen går mod 0. Det er korrekt, at notationen i integralet

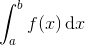
$\int_{a}^{b}f(x)\, \textup{d}x$

skal minde os om denne grænseværdi

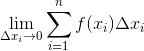
$\lim_{\Delta x_{i}\rightarrow 0}\sum_{i=1}^{n}f(x_{i})\Delta x_{i}$

Skriv et svar til: integrere ved substitution

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.