Matematik
Kompleks andengradsulighed
Jeg håber virkelig, nogen kan hjælpe mig med denne opgave:
Bestem alle de løsninger for den komplekse ligning:
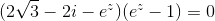 ,
,
som har en absolutværdi, der er mindre end 2π.
Jeg er indtil videre kommet frem til, at jeg via nulreglen skal løse ligningerne:
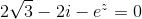 og
og 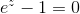 .
.
Den første har jeg fået til:
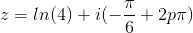
Og den sidste:
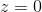 .
.
Jeg har så prøvet, at vælge de løsninger, for hvilke |z| < 2π:
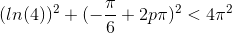 ,
,
ved at løse andengradsligningen:
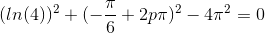 .
.
Men jeg ved simpelthen ikke, hvordan jeg skal løse den i hånden. Og jeg ved heller ikke, hvordan jeg opstiller ligningen for z=0.
Hvad skal jeg gøre?
Svar #1
24. september 2016 af VandalS
Se https://www.studieportalen.dk/forums/thread.aspx?id=1703324
Svar #3
24. september 2016 af VandalS
Vinklen til 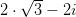 kan du finde ved at tage
kan du finde ved at tage 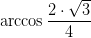 og
og 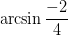 , og derefter finde den vinkel de har til fælles. Find herefter vinklen hovedargument.
, og derefter finde den vinkel de har til fælles. Find herefter vinklen hovedargument.
Svar #5
24. september 2016 af VandalS
Hvis du blindt taster det ind på en lommeregner, ja. Men husk, at der generelt er to vinkler med den samme cosinusværdi, og to vinkler med den samme sinusværdi. Det er et spørgsmål om fortegn, som du kan se ved at lave en skitse af enhedscirklen og tegne vinklerne ind. Du kan også ud af hvilken vinkel der er den rigtige ved at se på hvilken kvadrant, det komplekse tal ligger i.
Svar #6
24. september 2016 af miesim1 (Slettet)
Nu forstår jeg. Men, hvis -π/6 og 11π/6 er "det samme", hvorfor er -π/6 så ikke korrekt?
Svar #7
24. september 2016 af VandalS
Begge dele kommer til at indgå i dine løsninger, men der er forskel på 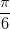 og
og 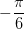 .
.
Svar #8
24. september 2016 af miesim1 (Slettet)
Ja, jeg kan godt se, at tallet ligger i fjerde kvadrant, men da vinklerne -π/6 og 11π/6 har samme cosinus- og sinusværdi, hvorfor er -π/6 så ikke også korrekt?
Svar #9
24. september 2016 af VandalS
De er den også, og du skal angive begge når du angiver alle løsninger. Medmindre man har fået besked på at gøre sådanne angiver man dog som regl kun den ene, hvis vinkel er i 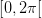 .
.
Svar #10
24. september 2016 af miesim1 (Slettet)
Åhh, okay :) Det giver selvfølgelig god mening. Så der er indtil videre to løsninger, hvordan finder jeg de andre, og hvordan ved jeg, hvilken der er korrekt inden for de 2π? - skal jeg bare blive ved med at lægge 2π til?
Svar #11
24. september 2016 af miesim1 (Slettet)
Skal det forstås på den måde, at der vel egentlig kun er én løsning, eftersom løsningen skal ligge inden for 2π?
Svar #12
24. september 2016 af VandalS
"
#10 Betragt det simplere problem 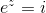 . Da
. Da 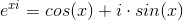 er hovedargument
er hovedargument 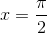 , men da sinus-funktionen og cosinus-funktionen er periodisk med
, men da sinus-funktionen og cosinus-funktionen er periodisk med 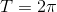 har opgaven uendeligt mange løsninger af formen
har opgaven uendeligt mange løsninger af formen 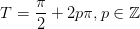 . Det er der tilsvarende også i din opgave, men kun nogle af disse uendeligt mange løsninger har en længde (absolutværdi), der er mindre end
. Det er der tilsvarende også i din opgave, men kun nogle af disse uendeligt mange løsninger har en længde (absolutværdi), der er mindre end 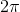 . Opgaven beder dig angive denne mindre mængde.
. Opgaven beder dig angive denne mindre mængde.
"
Svar #13
24. september 2016 af miesim1 (Slettet)
Kan det passe, at de løsninger, der har en absolutværdi, som er mindre end 2π er:
11π/6, -π/6 og 13π/6?
Svar #14
24. september 2016 af miesim1 (Slettet)
Eller er 13π/6 egentlig inkluderet, eftersom dens absolutværdi=2π?
Svar #16
24. september 2016 af VandalS
Du skal i øvrigt ikke tænke så meget på vinklernes størrelse. Opgaven spørger til tallene  's absolutværdi.
's absolutværdi.
Svar #17
24. september 2016 af miesim1 (Slettet)
Jeg har læst tråden.
Min konklusion er så, at de løsninger, der har en absolutværdi, som er mindre end 2π er:
11π/6 og -π/6.
Men eftersom tallet ligger i fjerde kvadrant, er de endelige løsninger:
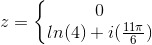
Er det korrekt?
Svar #18
24. september 2016 af VandalS
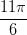 og
og 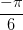 er vinkler, så de er ikke den hele løsning. Du skal finde de komplekse tal, der løser din ligning. Dem du har listet af to ud af de tre løsninger hvis absolutværdi er mindre end
er vinkler, så de er ikke den hele løsning. Du skal finde de komplekse tal, der løser din ligning. Dem du har listet af to ud af de tre løsninger hvis absolutværdi er mindre end 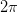 .
.
Svar #19
24. september 2016 af miesim1 (Slettet)
Jeg har, at:
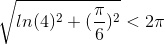
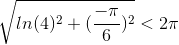
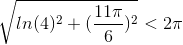
Det er vel de tre løsninger, hvis absolutværdi er mindre end 2π?
Svar #20
24. september 2016 af miesim1 (Slettet)
Jeg er temmelig forvirret. Vil du ikke nok være sød at fortælle, hvad det rigtige svar er?






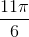 fra?
fra?