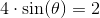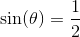Matematik
Side 2 - Kompleks andengradsulighed
Svar #22
24. september 2016 af VandalS
Var væk fra computeren mens jeg var ved at gøre mig klar til at gå i seng.
Her er fremgangsmåden til opgaven:
Vi skal løse ligningen
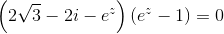 .
.
Ifølge nulreglen er dette tilfældet når enten den ene eller den anden parentes er nul, så vi løser hver for sig.
Den simple parentes giver os, at
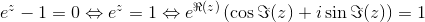 .
.
Da der ikke optræder en imaginær komponent på højresiden må 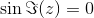 , og da den eksponentielle skaleringsfaktor ikke kan være negativ må
, og da den eksponentielle skaleringsfaktor ikke kan være negativ må 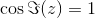 . Dette betyder, at
. Dette betyder, at 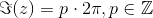 . Desuden har vi at
. Desuden har vi at 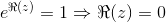 . En familie af løsninger
. En familie af løsninger 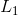 er derfor
er derfor 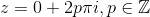 .
.
Den anden parentes giver os, at
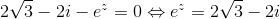
Løsningen af dette har vi gennemgået, og familien af løsninger 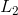 er
er
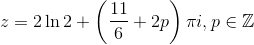 .
.
Ud af disse to familier af uendeligt mange løsninger skal vi så finde dem, der har absolutværdi mindre end 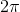 . Du kan hurtigt kontrollere, at de eneste løsninger, der opfylder kravet er
. Du kan hurtigt kontrollere, at de eneste løsninger, der opfylder kravet er
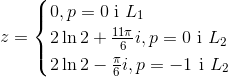 ;
;
Dette er det endelige svar på opgaven.
Svar #24
24. september 2016 af miesim1 (Slettet)
Tusind, tusind tak! :) Du har virkelig været til stor hjælp.
Svar #26
24. september 2016 af miesim1 (Slettet)
Ja, bestemt. Jeg er selv på vej i seng. Sov godt :)
Skriv et svar til: Kompleks andengradsulighed
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.






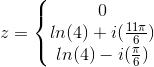
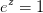
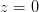
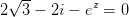
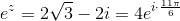
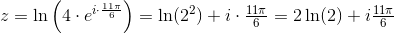
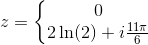

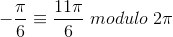
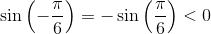 i modstrid med
i modstrid med