Matematik

Rækker,

20. maj 2017 af Rossa - Niveau: Universitet/Videregående

Hej derude, er i gang med en opgave, som er svært for mig. Desværre har jeg ikke gode forudsætning til at løse opgaven.

Vil nogen derude hjælpe med opgaven?

Opgaven lyder:
Lad p > 0 og betragt rækken:

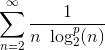
$\sum_{n=2}^{\infty} \frac{1}{n \ \log_2^p(n)}$

Find de værdier af p, for hvilke rækken er konvergent.

På forhånd tak

Brugbart svar (1)

Svar #1
20. maj 2017 af fosfor

Samtlige led i summen er positive og aftagende mht. p, så hvis summen er konvergent med p₀ så er den det også med alle større p, og hvis den er divergent med p₀ så er den er divergent med alle mindre p.

Vis derfor at den er divergent med p=1 og konvergent med p=1+ε

Svar #2
20. maj 2017 af Rossa

Hvorfor konkluderer du, at følgen vil divergere med p=1 og konvergere med p=1+ε.
Hvad er den sætning du bruger, da jeg kan se, at svaret er rigtigt, men argumentationen mangler jeg

Brugbart svar (1)

Svar #3
20. maj 2017 af AskTheAfghan

Se Cauchy Condensation Test.

Brugbart svar (1)

Svar #4
20. maj 2017 af fosfor

Tegn funktionen 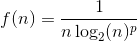$f(n)=\frac{1}{n \log_2(n)^p}$ fra n=2 til n=∞

For alle heltal n>=3 kan du tegne rektangler med hjørnerne (n, f(n)) og (n-1, 0), som har areal f(n).

Summen (minus det første led) svarer til det samlet areal af disse rektangler.

Da alle rektangler ligger under grafen (da den er aftagende) er summen mindre end arealet af f(n) fra n=2 til n=∞.

Svar #5
20. maj 2017 af Rossa

Jeg tror, at jeg skal lave opgaven på følgende måde:
Fra: 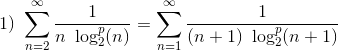$1 ) \ \sum_{n=2}^{\infty} \frac{1}{n \ \log_2^p(n)}= \sum_{n=1}^{\infty} \frac{1}{(n+1) \ \log_2^p(n+1)}$

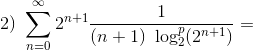$2 ) \ \sum_{n=0}^{\infty} 2^{n+1} \frac{1}{(n+1) \ \log_2^p(2^{n+1})}=$ og det skal formuleres til geometriske række, hvor |r| skal afhænge af p, og p skal gøre |r| mindre end 1.

Det kan jeg ikke formulere til en geomtriske række

Brugbart svar (1)

Svar #6
20. maj 2017 af Soeffi

#3 Cauchy's kondensationtest virker oplagt at bruge.

Antag at du har en talfølge {a_n} af positive led, der hele tiden bliver mindre og mindre. Der gælder, at

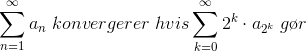
$\sum_{n=1 }^{\infty }a_n\;konvergerer\;hvis\sum_{k=0 }^{\infty }2^k\cdot a_{2^k}\;g\o r$

Her starter summen ganske vist med n=2, men det må være underordnet. Man får med n = 2^k:

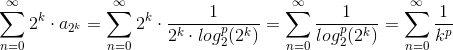
$\\\sum_{n=0 }^{\infty }2^k\cdot a_{2^k} =\sum_{n=0 }^{\infty }2^k\cdot\frac{1}{2^k\cdot log^p_2(2^k)} =\sum_{n=0 }^{\infty }\frac{1}{log^p_2(2^k)} = \sum_{n=0 }^{\infty }\frac{1}{k^p}$

Denne række er konvergent for p > 1. Det udelukker dog ikke, at der kan være værdier for 0 < p ≤ 1, hvor rækken er konvergent.

Svar #7
20. maj 2017 af Rossa

Tak til alle sammen nu. Problemet nu er, at forstå, at min n starter i 2 og ikke i 1, efter definitionen.

Brugbart svar (1)

Svar #8
20. maj 2017 af Therk

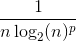
$\frac{1}{n \log_2(n)^p}$

er endeligt for n = 1 og for alle p. Dvs. om du har det med eller ej er ligegyldigt for din betragtning om summen er endelig.

Brugbart svar (1)

Svar #9
20. maj 2017 af Soeffi

#6 Rettelse:
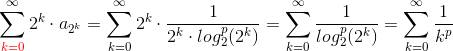
$\sum_{{\color{Red} k=0} }^{\infty }2^k\cdot a_{2^k} =\sum_{k=0 }^{\infty }2^k\cdot\frac{1}{2^k\cdot log^p_2(2^k)} =\sum_{k=0 }^{\infty }\frac{1}{log^p_2(2^k)} = \sum_{k=0 }^{\infty }\frac{1}{k^p}$

Brugbart svar (0)

Svar #10
21. maj 2017 af Stats

Benyt omskrivningen 2^log₂(n) = n ⇔ ln(2^log₂(n)) = ln n ⇔ log₂(n)·ln(2) = ln n ⇔ log₂(n) = log₂ n = ln(n)/ln(2)

Altså

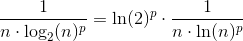
$\frac{1}{n\cdot\log_2(n)^p}=\ln(2)^p\cdot\frac{1}{n\cdot \ln(n)^p}$

ln(2)<1 - - Hvorfor? Fordi ln(e⁰) = 0 og ln(e¹) = 1 og 1 < 2 < e

Derfor er

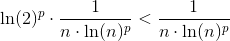
$\ln(2)^p\cdot\frac{1}{n\cdot \ln(n)^p}<\frac{1}{n\cdot\ln(n)^p}$

På side 706 i TL har vi opgaven:

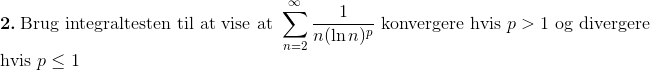
$\\ \textbf{2.}\ \textup{Brug integraltesten til at vise at }\sum_{n=2}^{\infty}\frac{1}{n(\ln n)^p} \textup{ konvergere hvis }p>1\textup{ og divergere}\\ \textup{hvis }p\leq 1$

- - -

Mvh Dennis Svensson

Brugbart svar (0)

Svar #11
21. maj 2017 af Stats

Integraltesten

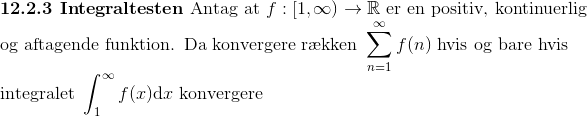
$\\ \textbf{12.2.3 Integraltesten}\textup{ Antag at }f:[1,\infty)\to\mathbb{R}\textup{ er en positiv, kontinuerlig}\\ \textup{og aftagende funktion. Da konvergere r\ae kken }\sum_{n=1}^{\infty}f(n)\textup{ hvis og bare hvis}\\ \textup{integralet }\int_{1}^{\infty}f(x)\mathrm dx\textup{ konvergere}$

- - -

Mvh Dennis Svensson

Brugbart svar (0)

Svar #12
21. maj 2017 af Stats

$\\ \int_{2}^{\infty}\frac{1}{n}(\ln n)^{-p}=\left [ (\ln n)\cdot (\ln n)^{-p}\right ]_2^\infty-\int_{2}^{\infty}\ln n\left ( -p(\ln n)^{-p-1}\cdot\frac{1}{n} \right )\\ =\left [(\ln n)^{-p+1}\right ]_2^\infty+p\int_{2}^{\infty}(\ln n)^{-p}\cdot\frac{1}{n}$

Vi trækker integralet fra på begge sider

$\\ \int_{2}^{\infty}\frac{1}{n}(\ln n)^{-p}=\left [(\ln n)^{-p+1}\right ]_2^\infty+p\int_{2}^{\infty}(\ln n)^{-p}\cdot\frac{1}{n}\\ 0=\left [(\ln n)^{-p+1}\right ]_2^\infty+\left ( p-1 \right )\int_{2}^{\infty}(\ln n)^{-p}\cdot\frac{1}{n}\\ \frac{\left [(\ln n)^{-p+1}\right ]_2^\infty}{p-1}=\int_{2}^{\infty}\frac{1}{n}(\ln n)^{-p}$

For hvilke p er integralet begrænset?

$\frac{1}{p-1}\left [ (\ln n)^{1-p} \right ]_2^\infty=\frac{1}{p-1}\left [ (\ln \infty)^{1-p}-(\ln 2)^{1-p} \right ]$

(Undskyld notationen), Men det er nu indlysende at rækken konvergere for p>1

- - -

Mvh Dennis Svensson

Skriv et svar til: Rækker,

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.