Lige nu 109 online.

Persondatapolitik

Studieportalen.dk › Kompendier › Matematik › Matematik formelsamling › Procentregning › Hvordan regner man procent

Hvordan regner man procent

Man kan regne med procent på flere forskellige måder. Simpel beregning af procent kan ske på baggrund af en brøk. Når man ser delværdien (tælleren) 1 og hele værdien (nævneren) 2, som er lig med brøken $\frac{1}{2}$ , tænker de fleste, at det svarer til 50 %.

Der er også mange andre simple brøker, som hurtigt kan omsættes til et procenttal og omvendt. Se endvidere procent til brøk i artiklen procent.

Helt grundlæggende er der to forskellige måder at regne med procenter på.

Hvordan regner man procent, når man har to værdier og en procentdel, og for det andet, hvordan regner man procent ud, når man skal sammenligne to værdier procentvis?

Den første type kalder vi 'beregning af procent'. Den anden type, der handler om stigning i procent, fald i procent og ændring i procent, vil blive behandlet under artiklerne Procentvis stigning og Procentvis ændring.

Beregning af procent

Den bedste måde at starte på, er ved at forstå logikken i procentregning. Der gælder den helt fundamentale regel at:

'en delværdi gange $100 \%$ er lig med en hel værdi gange procentdelen'.

Bruger vi eksemplet fra indledningen svarer det til at delværdien 1 gange 100 % på den ene side af lighedstegnet er lig med (hel)værdien 2 gange 50 % på den anden side (100 = 100).

Forstår man logikken med en hel værdi, delværdi og en procentdel er man kommet langt i at forstå procentregning. Dette er nemlig logikken, som ligger til grund for størstedelen af tilfælde, hvor man skal lave regning med procent.

Vi kalder delværdien for y, hele værdien for x, og procentdelen for z.

På en formel ser det således ud:

$y \cdot 100 \% = x \cdot z (\%)$

Denne formel kan opstilles på tre forskellige måder, alt efter hvilken variabel der en den ukendte.

$y = \frac {x}{100 \%} \cdot z (\%)$ (man udregner en delværdi y)

$x = \frac {y}{z (\%)} \cdot 100 \%$ (man udregner den hele værdi x)

$z (\%)= \frac {y}{x} \cdot 100 \%$ (man udregner procentdelen z)

Logikken kan måske eksemplificeres yderligere med brøken $\frac {7}{8}$ :

Delværdien 7 gange 100 % på den ene side af lighedstegnet er lig med hele værdien 8 gange procentdelen z.

Den procentdel z, som brøken $\frac {7}{8}$ svarer til, kan nu beregnes.

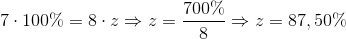
$7 \cdot 100 \% = 8 \cdot z \Rightarrow z = \frac{700 \%}{8} \Rightarrow z = 87,50 \%$

Længere nede i artiklen kan du i eksempel 1-3 se de forskellige typer af beregning med procent.

Det omvendte tilfælde med procent

Derudover kan man lave procentregning, hvor man skal finde den procentdel, som helværdien x udgør af delværdien y. Det vil sige det omvendte af det skitserede ovenfor.

Hvor mange procent udgør værdien x af delværdien y, opstilles på denne formel:

$z (\%) = \frac {x}{y} \cdot 100 \%$ (man udregner procentdelen z)

Det er afgørende at fastslå, at denne formel ikke kan omskrives til den grundlæggende formel ovenfor, da mængderne har bibeholdt de samme notationer (x = hele værdien og y = delværdien) for at forsimple logikken. Se eksempel 4.

Da tal er med til at øge overskueligheden og forståelsen, følger herunder et eksempel for hver af de formler, for at forstå den kontekst, hvor de kan benyttes. Til slut i eksempel 5 en måde hvorpå man kan trække procent fra eller lægge procent til i eksempel 6.

Eksempler på beregning af procent

Hvor meget er 44 % af det samlede beløb på 2625 kr.? (x = 2625 kr. og z = 44 %)

$y = \frac{x}{100 \%} \cdot z (\%) \Leftrightarrow y = \frac{2625 kr.}{100 \%} \cdot 44 \% \Leftrightarrow y = 1155$ kr.

Resultatet er 1155 kr.

I denne beregning kan det hjælpe at tænke på, at 2625 kr. er hele værdien på 100 %. 1 % af hele værdien 2625 kr. er en hundrededel, og den kan findes ved at dividere med 100 % eller rykke kommaet to pladser til venstre. 1 % = 26,25 kr. For at finde 44 % skal man derfor gange 26,25 kr. med 44 for at finde størrelsen på delværdien.
Man har brugt 1020 kr. og de udgør 17 % af det samlede budget. Hvad er hele beløbet, der er til rådighed i budgettet? (y = 1020 kr. og z = 17 %)

$x = \frac{y}{z (\%)} \cdot 100 \% \Leftrightarrow x = \frac{1020 kr.}{17 \%} \cdot 100 \% \Leftrightarrow x = 6000$ kr.

Det samlede beløb i budgettet er 6000 kr.

Her kan det hjælpe at tænke på, at de 1020 kr. er en delværdi, der udgør 17 %. For at finde en hundrededel eller 1 % skal man dividere 1020 kr. med 17 %. Så har man udregnet værdien i kr. for 1 %, og skal nu gange den med 100 % for at finde hele værdien i kr.
Hvor mange procent udgør 45 kr. af 750 kr.? (y = 45 kr. og x = 750 kr)

$z (\%)= \frac{y}{x} \cdot 100 \% \Leftrightarrow z = \frac{45 kr.}{750 kr.} \cdot 100 \% \Leftrightarrow z = 6 \%$

De udgør præcis 6 % af det samlede beløb.

Her skal man tænke på forholdet mellem to værdier, hvor man skal finde procentdelen. Det svarer til at opstille de to tal som en brøk, og derefter gange med 100 % for at finde procentdelen.

I lommeregneren kan du selv indsætte den brøk, som du skal omregne til en procentdel. I værdi 1 indsættes tælleren, og i værdi 2 indsættes nævneren i brøken.

Denne formel kan benyttes både hvor nævneren er størst som her, men også hvor tælleren er størst som i eksempel 4 herunder.
Hvor mange procent udgør 800 kr. af 250 kr.? (y = 800 kr. og x = 250 kr.)

$z (\%) = \frac{x}{y} \cdot 100 \% \Leftrightarrow z = \frac{800 kr.}{250 kr.} \cdot 100 \% \Leftrightarrow z = 320 \%$

De udgør 320 % af beløbet.

Samme grundidé som eksempel 3. Ligegyldig hvilken værdi, der er størst skal de to værdier forholdes til hinanden og ganges med 100 %.
Hvordan regner man procent, når man skal trække procent fra:

Træk 15 procent fra 260 kr.?

Når man skal trække procent fra en hel værdi, skal man reelt udregne værdien af resten (delværdien), dvs. 100 % - 15 % = 85 %.

$\frac{260 kr.}{100 \%} \cdot 85 \% = 221$ kr.
Hvordan regner man procent når man skal lægge procent til:

Læg 15 procent til 260 kr.?

Når man skal lægge procent til en delværdi, skal man reelt udregne hele værdien, dvs. 100 % + 15 % = 115 %.

$\frac{260 kr.}{100 \%} \cdot 115 \% = 299$ kr.

Læs mere om Udregning af procent, lær om Momsberegning og se derudover artiklen Procentregning - opgaver.

Indhold

Seneste indlæg
9: Hjælp til at snakke tysk (0)
9: Hævn og tilgivelse religion (2)
A: Syre-base (0)
B: Måling af halveringstid (0)
B: Måling af halveringstid (0)

Populære indlæg
B: Måling af halveringstid - forsøg (16)
9: Hjælp til at snakke tysk (0)
9: Hævn og tilgivelse religion (2)
V: beregningsopgaver (3)
8: Dele 125000 i forholdet 20 : 30 (3)

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se