Brøkregning
Brøkregning beskriver, hvordan man regner med brøker. Det vil sige operationer som addition, subtraktion, division og multiplikation af brøker.
I denne artikel vil vi gennemgå de grundlæggende operationer, addition og subtraktion. For division af brøker se artiklen Dividere brøker. For multiplikation af brøker se artiklen Hvordan ganger man brøker?
Hvad er en brøk?
En brøk er to tal divideret med hinanden. De to tal skal være det, man kalder heltal. Heltal er tal, som ikke har noget komma. Altså er 9, 28, 537, 1.482, 13.489 og -40 heltal, men 3,3 er ikke.
Brøker skrives normalt med brøkstreg:
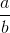
Vi kalder tallet over brøkstregen for brøkens tæller og tallet under brøkstregen for brøkens nævner.
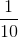
Her er 1 brøkens tæller og 10 brøkens nævner. Man kan også sige, at ovenstående er én tiendedel. Altså nævneren siger, hvor store delene er, og tælleren siger, hvor mange vi har.
Man deler brøker op i to typer: ægte brøker og uægte brøker (link).
En ægte brøk er en brøk, som giver os et kommatal mellem 0 og 1. Det eneste vi kræver for at have en ægte brøk, er at tæller er mindre end nævner.
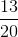
Ovenstående er altså en ægte brøk, fordi 13 er mindre end 20, og hvis man regner brøken ud som et kommatal, får man 0,65.
En uægte brøk er en brøk, som ikke opfylder, at tæller er mindre end nævner.
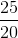
Her er 25 større end 20, hvilket vil sige, at dette er en uægte brøk. Hvis man regner denne brøk ud som kommatal, får man 1,25.
En uægte brøk kan omskrives til et såkaldt blandet tal, hvilket betyder, at vi får et heltal og en ægte brøk. 25 går op i 20 én hel gang, og derefter vil der være 5 tyvendedele tilbage:
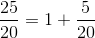
Man skriver altså et blandet tal som et heltal plus en ægte brøk.
Brøker kan forlænges, hvilket betyder, at man gør både tæller og nævner større ved at gange med et tal:
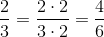
Her ganger vi tæller og nævner med 2. At forlænge en brøk ændrer ikke noget på dens værdi, så længe man sørger for at gange med det samme tal i både tæller og nævner. Derfor kan man forlænge, så meget man vil. Ofte forlænger man for at få at give to brøker fællesnævner.
Man kan også forkorte brøker, hvilket fungerer på samme måde, bortset fra at man dividerer i stedet for at gange, og derfor får man mindre tæller og nævner.
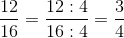
Vi kan dividere både 12 og 16 med 4, og få heltal, hvilket giver os en forkortet brøk. I de fleste tilfælde vil man forkorte en brøk, hvis det er muligt. En forkortet brøk er nemmere at overskue og regne med.
Addition af brøker
Når man vil lægge to brøker sammen, skal man altid sørge for, at de har fællesnævner. Altså den ene brøks nævner skal være den samme som den anden brøks nævner.
Hvis to brøker har fællesnævner, skal man bare lægge deres tællere sammen:
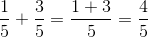
Her har vi en femtedel og tre femtedele, som vi skal lægge sammen, hvilket altså bare er fire femtedele.
Hvis vi skal lægge to brøker sammen, som ikke har samme nævner, bliver vi nødt til at forkorte og/eller forlænge dem, så de får fællesnævner.
Lad os se på nogle eksempler:
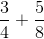
Her har vi to forskellige nævnere 4 og 8. Det er dog meget ligetil at få fællesnævner, da vi ved, at 8 er det dobbelte af 4. Altså kan vi forlænge den første brøk med 2:
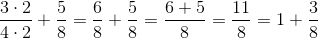
Vi forlænger altså den ene brøk, så de begge har samme nævner, og så regner vi additionen ligesom før. Til sidst laver vi den uægte brøk om til et blandet tal.
I nogle tilfælde har vi dog at gøre med to brøker, hvor man ikke umiddelbart ser en sammenhæng mellem nævnerne. Her kan man blive nødt til at forlænge eller forkorte begge for at få fællesnævner.
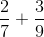
Ovenstående har vi et eksempel på en sådan brøkaddition. Det mest ligetil at gøre, hvis man ikke kan se noget begge nævnere går op i, er at gange de to nævnere.
9 gange 7 giver 63. Vi kan altså bruge 63 som fællesnævner, da begge nævnere går op i denne. Det vil sige, vi skal forlænge den første brøk med 9 og den anden brøk med 7.
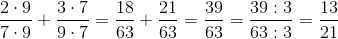
Vi forlænger altså brøkerne, lægger dem sammen og til sidste ser vi at tæller og nævner begge går op i 3, så vi forkorter brøken.
Subtraktion af brøker
I brøkregning har minus samme metode som plus. Nemlig at vi først finder fællesnævner og dernæst foretager udregningen mellem brøkkernes tællere. Således:
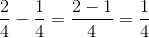
Altså vi trækker bare de to brøker fra hinanden i tælleren.
Brøkopgaver
Vi vil nu se på par opgaver med brøker.
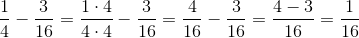
Vi har to brøker, der skal trækkes fra hinanden. For at få fællesnævner forlænger vi den første brøk 4 gange, og derefter kan vi trække de to brøker fra hinanden.
I den anden opgave vil vi se på, hvad man gør, hvis man har flere end to brøker:
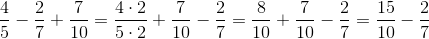
Vi har tre brøker, der skal trækkes fra og lægges til hinanden. De har ikke fællesnævner. Man kan skabe fællesnævner ved at gange alle de tre nævnere sammen, men det ville give nogle ret store tal. Så i stedet løser vi problemet ved at skabe fællesnævner mellem brøkerne to af gangen.
Vi har altså forlænget og lagt sammen, så vi nu bare har to brøker som skal trækkes fra hinanden.
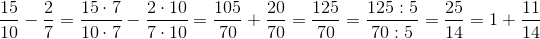
Vi skaber fællesnævner ved at forlænge med den anden brøks nævner. Vores resultat giver en tæller og nævner, der begge går op 5, så vi forkorter, og til sidste skriver vi resultatet som et blandet tal.

