Matematik

Cirkel og tangent

22. september 2015 af hanshansen123456 (Slettet) - Niveau: A-niveau

En cirkel har ligningen (x-3)²+(y-5)²=25. og en ligning m har ligningen y=4/3x.

a) gør rede for at førsteaksen er en tangent til cirklen.

b) Cirklen har to tangenter, der er parallele med linjen m.

Bestem koordinatsættene til hvert af de to røringspunkter for tangenterne.

Brugbart svar (0)

Svar #1
22. september 2015 af PeterValberg

a) indsæt y = 0 i cirklens ligning og løs mht. x, hvis der kun er én løsning, så er førsteaksen tangent

- - -

mvh.

Peter Valberg
(YouTube)

Brugbart svar (0)

Svar #2
22. september 2015 af mathon

a) gør rede for at førsteaksen er en tangent til cirklen.

      Cirklens centrum er (3,5) og radius r = 5. Centrums afstand til x-aksen er derfor 5 = r
og
      centrums projektion på x-aksen 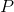er (3,0), som ligger på cirklen, da

                (3-3)²+(0-5)² = 5²
endvidere er

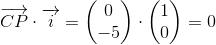
$\overrightarrow{CP}\cdot \overrightarrow{i}=\begin{pmatrix} 0\\-5 \end{pmatrix}\cdot \begin{pmatrix} 1\\0 \end{pmatrix}=0$

hvorfor
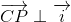
$\overrightarrow{CP}\perp \overrightarrow{i}$

x-aksen står derfor vinkelret på radius i røringspunktet 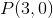P(3,0) , hvorfor x-aksen er tangent til
cirklen:
(x - 3)² + (y - 5)² = 5²

Brugbart svar (0)

Svar #3
22. september 2015 af mathon

Brugbart svar (0)

Svar #4
22. september 2015 af mathon

En retningsvektor for de to søgte tangenter
er:
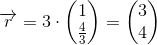
$\overrightarrow{r}=3\cdot \begin{pmatrix} 1\\\frac{4}{3} \end{pmatrix}=\begin{pmatrix} 3\\4 \end{pmatrix}$

Tangentkravet er for røringspunktet 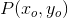P(x_o,y_o) :
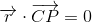
$\overrightarrow{r}\cdot \overrightarrow{CP}=0$

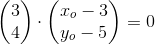
$\begin{pmatrix} 3\\4 \end{pmatrix}\cdot \begin{pmatrix} x_o-3\\y_o-5 \end{pmatrix}=0$

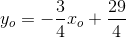
                              $y_o=-\frac{3}{4}x_o+\frac{29}{4}$
som indsat i cirklens ligning
giver:
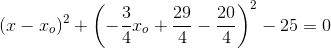
                               $(x-x_o)^2+\left ( -\frac{3}{4}x_o+\frac{29}{4}-\frac{20}{4} \right )^2-25=0$
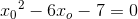
                               ${x_{0}}^{2}-6x_o-7=0$
hvoraf røringspunkterne
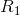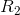                               R_1 og R_2 kan beregnes af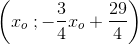 $\left (x_o\; ; -\frac{3}{4}x_o+\frac{29}{4} \right )$

Brugbart svar (0)

Svar #5
22. september 2015 af mathon

alternativt:

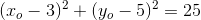(x_o-3)^2+(y_o-5)^2 = 25 som differentieret
giver
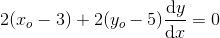$2(x_o-3)+2(y_o-5)\frac{\mathrm{d} y}{\mathrm{d} x} = 0$ som divideres med 2

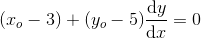
$(x_o-3)+(y_o-5)\frac{\mathrm{d} y}{\mathrm{d} x} = 0$

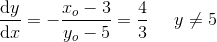
$\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{x_o-3}{y_o-5}=\frac{4}{3}\; \; \; \; \; y\neq5$
hvoraf
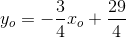
$y_o=-\frac{3}{4}x_o+\frac{29}{4}$

og resten som i #4.

Brugbart svar (0)

Svar #6
17. oktober 2015 af AnnaLinde (Slettet)

Hej, må jeg spørge, hvordan i får lavet opg b.?

Jeg står med den i en aflevering og forstår intet. Det ville være skønt, hvis i også kunne forklare, hvorfor i gør det ;)

Mange tak

Brugbart svar (0)

Svar #7
08. oktober 2017 af scienceman1981

mathon, Måske et dumt spørgsmål men hvorfor ganger du retningsvektoren for l med en faktor 3?

Brugbart svar (0)

Svar #8
08. oktober 2017 af mathon

…fordi
retningsvektor $\small \overrightarrow{n}=\bigl(\begin{smallmatrix} 3\\4 \end{smallmatrix}\bigr)$ er meget mere bekvem.

Brugbart svar (0)

Svar #9
08. oktober 2017 af scienceman1981

Hej og tak for dit svar,

min hukommelse der er lidt tynd idag, men hvad der det for en regel som tillader at jeg må gange retningsvektoren for linjen med tallet 3?

Er det fordi cirklen skære i punktet (3,0)?

Brugbart svar (0)

Svar #10
08. oktober 2017 af mathon

Er vektor $\small \overrightarrow{r}$ en retningsvektor for en linje,
er vektorfamilien:
                                $\small \overrightarrow{r}_k=k\cdot \overrightarrow{r}$ retningsvektorer for linjen.

Brugbart svar (0)

Svar #11
08. oktober 2017 af mathon

tilføjelse:
$\small \small \overrightarrow{r}_k=k\cdot \overrightarrow{r}\; \; \; \; \; \; k\in\mathbb{R}$ retningsvektorer for linjen.

Skriv et svar til: Cirkel og tangent

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.