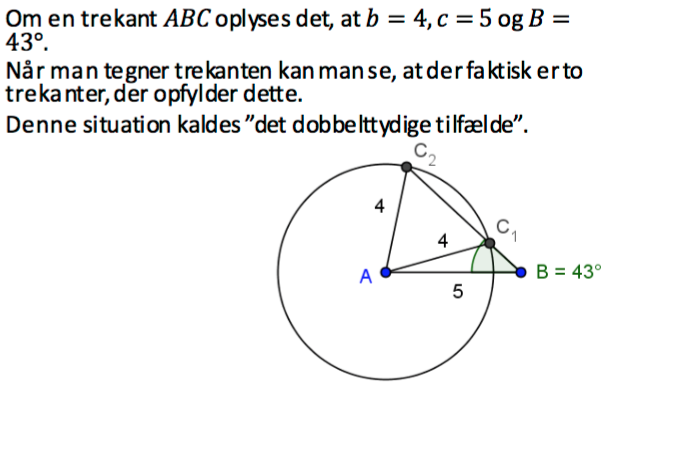
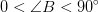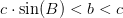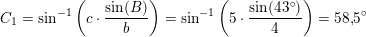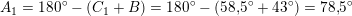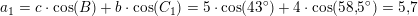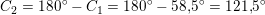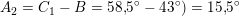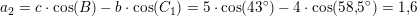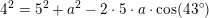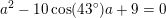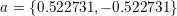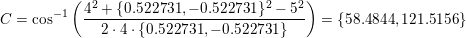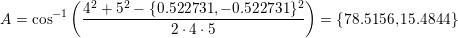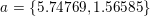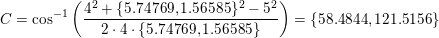Matematik

Det dobbelttydige tilfælde og enhedscirklen

24. juli 2017 af randomdude11 (Slettet) - Niveau: B-niveau

Hej jeg skal kunne redegøre for det dobbeltydig tilfælde.

Jeg har forstået vha. enhedscirklen, at udregning af vinkler med sinus relationer kan være dobbelttydigt i og med der er to løsninger og sinus vil have samme værdi til et spejlvendt punkt i 2.kvadrant.

Jeg er dog stødt på figuren (se vedhæftet), hvor der er to tilfælde, men begge er på højre side af cirklen. Burde C₂ ikke være spejlvendt i cirklen sådan, at det passet med (180-C₁) (180-43). Eller er det i forhold til B og er der i virkeligheden tre løsninger? Håber der er nogen der kan hjælpe med forståelsen/ uddybe figuren ift. enhedscirklen.

Tak for hjælpen på forhånd!

Vedhæftet fil: Screen Shot 2017-07-24 at 18.27.19.png

Brugbart svar (0)

Svar #1
24. juli 2017 af peter lind

Brugbart svar (1)

Svar #2
24. juli 2017 af peter lind

Nej. Du forveksler enhedscirklen med den tegnede cirkel. Det er en cirkel med centrum i A og radius 4. Det dobbelttydige kommer ind når man vil rene på det. Man bruger her sinusrelationen hvor C enten kan være vinnklen ved AC₂B eller AC₁B

Svar #3
24. juli 2017 af randomdude11 (Slettet)

#2
Nej. Du forveksler enhedscirklen med den tegnede cirkel. Det er en cirkel med centrum i A og radius 4. Det dobbelttydige kommer ind når man vil rene på det. Man bruger her sinusrelationen hvor C enten kan være vinnklen ved AC₂B eller AC₁B

Okay så cirklen her repræsentere hvordan de to tilfælde vil have forskellige længder IABI.

Hvis det var en enhedscirkel, ville C₂ være i 2 kvadrant og ville kunne løses som (180-C₁)? Så dobbeltydige tilfælde for sinus til vinklen, ville generelt ikke finde sted hvis vinklen er >90º, korrekt?

Brugbart svar (0)

Svar #4
24. juli 2017 af peter lind

Hvis man ad anden vej ved at vinklen er større end 90º eller for den sags skyld mindre end 90º vil der ikke være nogen dobbelttydighed

Brugbart svar (0)

Svar #5
24. juli 2017 af Eksperimentalfysikeren

Nej. Der gælder altid, at C₂ = 180º - C₁. Hvis de skulle ligge i enhedscirklen, skulle de ligge samme sted, og det gør de ikke. Iøvrigt er |AB| den samme i begge tilfælde. Det er BC₁, der er kortere end BC₂.

Hvad er det for en vinkel, du omtaler til sidst?

Svar #6
24. juli 2017 af randomdude11 (Slettet)

#5
Hvis de skulle ligge i enhedscirklen, skulle de ligge samme sted, og det gør de ikke.

Når du siger skulle de ligge samme sted, hvad mener du så helt præcis.

Hvad er det for en vinkel, du omtaler til sidst?

Hvis det var en enhedscirkel, ville C2 være i 2 kvadrant og ville kunne løses som (180-C1)?
(Jeg tænker på hvis overstående billede var en enhedscirkel)

Så dobbeltydige tilfælde for sinus til vinklen, ville generelt ikke finde sted hvis vinklen er >90º, korrekt?Jeg prøver at forstå hvornår der er tale om doobeltydige tilfælde for Sinus, eller om det altid er tilfældet. Da jeg har læst det kun sker nogle gange, hvilket forvirrer.

Brugbart svar (1)

Svar #7
24. juli 2017 af mathon

Det dobbelttydige tilfælde kræver:

$0<\angle B<90^\circ$
og
$c\cdot \sin(B)<b<c$

Brugbart svar (0)

Svar #8
25. juli 2017 af mathon

I det følgende er C₁ spids og C₂ stump.

    $\small \small C_1=\sin^{-1}\left ( c\cdot \frac{\sin(B)}{b} \right )=\sin^{-1}\left ( 5\cdot \frac{\sin(43^\circ)}{4} \right )=58{,}5^\circ$
    $\small A_1=180^\circ-(C_1+B)=180^\circ-(58{,}5^\circ+43^\circ)=78{,}5^\circ$
    $\small a_1=c\cdot \cos(B)+b\cdot \cos(C_1)=5\cdot \cos(43^\circ)+4\cdot \cos(58{,}5^\circ)=5{,}7$

    $\small C_2=180^\circ -C_1=180^\circ -58{,}5^\circ=121{,}5^\circ$
    $\small A_2=C_1-B=58{,}5^\circ-43^\circ)=15{,}5^\circ$
$\small a_2=c\cdot \cos(B)-b\cdot \cos(C_1)=5\cdot \cos(43^\circ)-4\cdot \cos(58{,}5^\circ)=1{,}6$

Brugbart svar (0)

Svar #9
26. juli 2017 af mathon

løst med cos-relationen:

$\small 4^2=5^2+a^2-2\cdot 5\cdot a\cdot\cos(43^\circ)$

$\small a^2-10 \cos(43^\circ)a+9=0$

$\small a=\{0{.}522731,-0{.}522731\}$

$\small C=\cos^{-1}\left ( \frac{4^2+\{0{.}522731,-0{.}522731\}^2-5^2}{2\cdot 4\cdot \{0{.}522731,-0{.}522731\}} \right )=\{58{.}4844,121{.}5156\}$

$\small A=\cos^{-1}\left ( \frac{4^2+5^2-\{0{.}522731,-0{.}522731\}^2}{2\cdot 4\cdot 5} \right )=\{78{.}5156,15{.}4844\}$

Brugbart svar (0)

Svar #10
26. juli 2017 af mathon

korrektion for tastefejl:

løst med cos-relationen:

$\small 4^2=5^2+a^2-2\cdot 5\cdot a\cdot\cos(43^\circ)$

$\small a^2-10 \cos(43^\circ)a+9=0$

$\small \small a=\{5{.}74769,1{.}56585\}$

$\small C=\cos^{-1}\left ( \frac{4^2+\{5{.}74769,1{.}56585\}^2-5^2}{2\cdot 4\cdot \{5{.}74769,1{.}56585\}} \right )=\{58{.}4844,121{.}5156\}$

$\small A=\cos^{-1}\left ( \frac{4^2+5^2-\{5{.}74769,1{.}56585\}^2}{2\cdot 4\cdot 5} \right )=\{78{.}5156,15{.}4844\}$

Brugbart svar (0)

Svar #11
26. juli 2017 af Eksperimentalfysikeren

#6:

Du skal være mere præcis. Du skriver "vinklen", men der er 3 vinkler i en trekant. Skriv A, B eller C i stedet for vinklen.

Du roder i vinklerne. Den cirkel, der er på figuren har centrum i A, mens det er vinkel C, der har to mulige cærdier C₁ og C₂, der opfylder C₂=180º - C₁.

Betingelsen for at det kan ske er, at vinkel B skal være spids. Desuden skal AC være kortere end AB. Prøv at tegne figuren med AC=6 i stedet for 4, og de andre værdier som på figuren.

Brugbart svar (0)

Svar #12
27. juli 2017 af mathon

Betingelsen for at det kan ske er, at vinkel B skal være spids. Desuden skal AC være kortere end AB, men længere end A's afstand til BC. Prøv at tegne figuren med AC=6 i stedet for 4, og de andre værdier som på figuren.

Brugbart svar (0)

Svar #13
27. juli 2017 af mathon

I en en anden formulering med samme indhold:

Det dobbelttydige trekantstilfælde kan opstå, når
det givne er
• en spids vinkel, dens modstående side og en af dens hosliggende sider
• den modstående side er kortere end den hosliggende side

Brugbart svar (0)

Svar #14
27. juli 2017 af mathon

#0
prøv evt. selv
                       I trekant ABC er
                          $\angle A=34{,}6^{\circ}\; \; \; \; a=5{,}7\; \; \; \; b=7{,}3$

Svar #15
28. juli 2017 af randomdude11 (Slettet)

#11
#6:

Du skal være mere præcis. Du skriver "vinklen", men der er 3 vinkler i en trekant. Skriv A, B eller C i stedet for vinklen.

Du roder i vinklerne. Den cirkel, der er på figuren har centrum i A, mens det er vinkel C, der har to mulige cærdier C₁ og C₂, der opfylder C₂=180º - C₁.

Betingelsen for at det kan ske er, at vinkel B skal være spids. Desuden skal AC være kortere end AB. Prøv at tegne figuren med AC=6 i stedet for 4, og de andre værdier som på figuren.

Jeg skriver, kun "vinklen", da jeg spørg ind til generelle regler, for hvornår en trekant er dobbelttydig. men tak for svar!

Skriv et svar til: Det dobbelttydige tilfælde og enhedscirklen

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.