Procent af et tal

Procent af et tal betyder generelt, at man tager en vis procentdel af et tal.

Man tager procent af et tal ved først at dele tallet op i 100 dele, og dernæst at gange antal procent med denne fraktion.

Skal man for eksempel finde 20 % af 500, finder man først 1 % således:

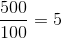
1 hundrededel eller 1 % af 500 er altså 5. Dernæst ganges 5 med 20 for at finde de 20 %:

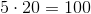
Man kan også skrive det hele som én udregning:

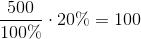
Altså som en generel formel for procent af tal kan man sige, at hvis man skal udregne procentdelen p af tallet x, gør man således:

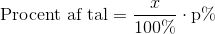
En anden måde, at forstå procent af et tal, er decimaltal, der skal angives i procent. Når man har et decimaltal og skal angive det i procent, skal man gange med 100 %. Eller med andre ord rykke kommaet to pladser til højre. Eksempelvis 0,28:

0,28 · 100% = 28 %

Det kan også sagtens være et decimaltal større end én, eksempelvis 1,56:

1,56 · 100 % = 156 %

Denne sammenhæng mellem procent og decimaltal, kan vi også bruge til at beregne procent af tal. Hvis omregner procentdelen til decimaltal, kan vi nemlig gange decimaltallet direkte på.

Hvis vi for eksempel vil finde 7 % af 354, kan vi skrive 7 % som decimaltallet 0,07. Derefter skal man gange dette på 354 for at få resultatet:

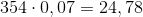
7 % af 354 er altså 24,78.

Eksempel 1

Hvis 90 % af ens kropsvægt består af vand, hvor mange kg vand indeholder en person med en vægt på 65 kg?

Dette kan vi nemt udregne ud fra det ovenstående princip. Vi deler 65 kg op i 100 dele og gange med 90:

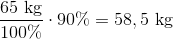
En person på 65 kg indeholder altså 58,5 kg vand.

Eksempel 2

Hvad er decimaltallet 3,542 i procent?

Som vi har set, skal vi bare gange med 100 for at få decimaltal som procent:

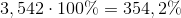
3,542 i decimaltal er altså det samme som 354,2 %

Eksempel 3

Elforbruget steg med 215 % af de oprindelige 700 kWh over 5 år.

Vi vil beregne stigningen:

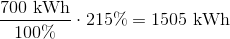
Elforbruget stiger altså med 1505 kWh over 5 år.

Husk at hvis man skal beregne det samlede elforbrug efter 5 år, skal man lægge de oprindelige 700 kWh til de 1505 kWh. Man kunne i dette tilfælde også bare lægge 100% til de 215 %, så ville man få det samlede forbrug efter 5 år.

Eksempel 4

Hvis mængden af vand i et bassin med 450 liter vand falder med 5%, hvor meget vand er der så tilbage?

Vi beregner først 5% af 450 liter:

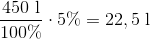
Bassinet mister altså 22,5 liter. Vi udregner hvor meget, der er tilbage, ved at trække 22,5 liter fra 450 liter:

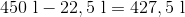
Dermed er der 427,5 liter vand tilbage i bassinet.