Fysik
Dynamik
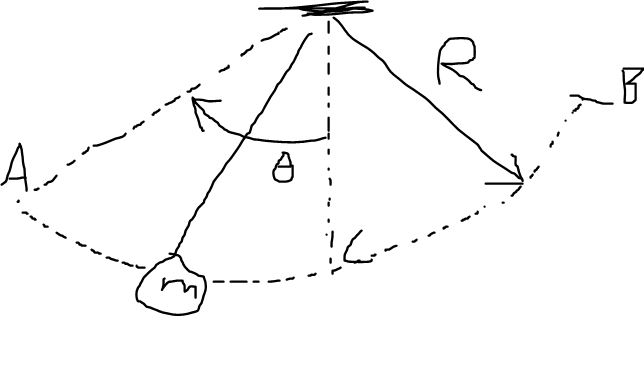
Forestil jer at i ser et pendul
Der skal findes Symbolsk et udtryk for kraften i pendulets kabel i yderpositionen A.
Svar #2
17. november 2019 af peter lind
Den totale kraft i derpositionen er 0, da den ikke bevæer sig. Denne resulerende kraft består dels af tyngdekrafen på lodde, som virkerlodret nedad, og dels snorekraften, som virker i snorens retning. Jeg har her forudsat at tyngdekraften på snoren kan sættes til 0
Svar #4
17. november 2019 af SuneChr
Loddet, med massen m, besidder i A Epot = mgh , hvor h er den lodrette niveauforskel for A og C .
h beregnes udtrykt ved R og udslagsvinklen Θ : h = R(1 - cos Θ)
Den kinetiske energi er 0 i loddets yderstillinger.
Svar #6
17. november 2019 af SuneChr
Under svingningen gælder sætningen for energibevarelse:
Epot + Ekin = konstant
Epot i C = 0 og Ekin i C = Epot i A
Svar #7
17. november 2019 af peter lind
#3 At den resulterende kraft er 0 hænger på MNewtons 2. lov. Der er ingen anden muligheder for for kræfter end de nævnte. Du kan bruge det til at finde hvor store de enkelte kræfter er
#7 Her er der kun kræfter i den lodrette retning. Desuden skal snoren levere den nødvendige centripetalkraft; men ellers gælder de samme regler der
Svar #9
17. november 2019 af peter lind
jo og desuden skal man kende snorens længde og tyngdeaccellerationen
Svar #10
17. november 2019 af ringstedLC
#8: I. flg. #0 skal du lave et udtryk, - ikke beregne noget.
Svar #11
18. november 2019 af Eksperimentalfysikeren
Der virker 2 kræfter på loddet: Tyngdekraften og snorekraften. Snorekraften består af to dele. Den ene del er tyngdekraftens komposant i snorretningen. Den anden del er centripetalkraften, der holde loddet i den cirkulære bane.
Hvis udsvinget er Θ, så er tyngekraftens komposant i snorens retning mg cos(Θ). Centriperalkraften er mv2/R. v kan findes ved energibetragtning. Den højde, loddet er hævet i forhold til ligevægtsstillingen, kalde h. Den er R(1-cos(Θ)). Det maksimale udsving kaldes Θmax. Ved denne stilling af pendulet er al energien potentiel. Ved andre udsving er energien en blanding af potentiel energi, Epot og kinetisk energi Ekin .Regnes potentiel energi ud fra hvilestillingen, fås Epot(Θ) = mgh = mg(1-cos(Θ)).
Ekin(Θ) = Epos(Θmax) - Epos(Θ) = ½mv2
Heraf kan du finde v2 udtrykt ved R, g, Θ og Θmax og der et udtryk for snorekraften, ved de samme størrelser.
Svar #12
19. november 2019 af chyvak
Jeg er ikke enig i at den samlede kraft i yderpositionerne er nul som nævnt i indlæg ovenfor. Hvis den var det, ville massen ikke kunne accelerere ud af disse positioner og dermed forblive der, da farten er nul. Alene det faktum at tyngden og snorkraften ikke er parallelle i disse positioner viser, at de ikke kan summere til nulvektoren.
Skriv et svar til: Dynamik
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.