Impuls
Impuls er en fysisk størrelse, der bestemmes af et legemes masse og hastighed. Impuls kaldes også bevægelsesmængde.
Impuls udregnes med følgende formel:
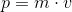
p er impuls
m er masse i kg
v er hastighed (velocitet) regnet i m/s
Impuls er altid bevaret når legemet ikke påvirkes af ydre krafter. Men selv ved påvirkning vil den samlede impuls altid forblive den samme. Det er fordi, impuls skal overholde energibevarelse - energi kan ikke forsvinde eller opstå, og impuls er kinetisk energi.
Impuls afhænger af et legemes hastighed, og af hvilken retning legemet bevæger sig i. Derfor vil impuls ofte tage form som en vektor. En vektor beskriver hvordan et punkt bevæger sig i det 2- eller 3-dimensionalt koordinatsystem.
.png)
Vektor i et 2-dimensionalt koordinatsystem. Vektoren har værdien (4, 3) da den bevæger sig 4 hen ad x-aksen og 3 hen af y-aksen.
For at beskrive i hvilken retning et legeme har en hastighed, bruger vi altså en vektor af 2 eller 3 dimensioner. Dette betyder, at impulsen også er en vektor og dermed har en retning. For at symbolisere at vi arbejder med en vektor, bruger vi en pil over variablen. Det giver os impulsformlen i vektorer:
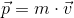
Impuls kan overføres fra legeme til legeme. Når et legeme med en impuls forskellig fra 0 rammer et andet legeme, kan en del af dets impuls overføres til det andet legeme, så det får en ny impuls.
I et lukket system vil der altid være impulsbevarelse, så en ændring i impuls af de to legemer skal i sidste ende give samme sum.
Hvis to legemer med hastighederne v1 og v2 rammer hinanden og ændrer hastighed til w1 og w2, forbliver summen den samme:
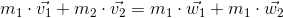
Hvis for eksempel to billard kugler rammer hinanden direkte, bliver de begge skudt tilbage. Vi kalder dette for elastisk stød, fordi den kinetiske energi er bevaret. Det vil sige, den kinetiske bevægelsesenergi som legemerne har, bliver ikke omdannet til andre former for energi. I virkeligheden vil dette ikke helt være tilfældet, da vi ikke har taget højde for friktion og lydenergi, men for billard kugler er det tæt nok til at vi kan betragte det som sådan.
Hvis de to kugler rammer hinanden lige på, og de har samme hastighed, må de også have samme hastighed efter stødet, men da de bliver skudt tilbage må hastighedsvektoren være drejet 180 grader.
Se eksempel 1.
Impulsmoment
Impulsmoment hænger tæt sammen med impuls. Forskellen er, at impulsmoment bevæger sig rundt om et punkt i stedet for ud af en linje.
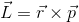
L er impulsmomentet
r er vektorkoordinaterne for legemets position i koordinatsystemmet ud fra centrum af banen
p er legemets impuls
Krydset betyder, at vi skal tage det såkaldte krydsprodukt eller vektorprodukt mellem de to vektorer r og p. Vi vil ikke gå nærmere ind på hvad krydsprodukter er og hvordan de regnes generelt, men blot give en formel for hvordan man udregner et tredimensionalt impulsmoment:
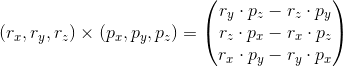
Krydsproduktet giver os altså endnu en vektor som er vores impulsmoment.
Eksempel 1
Vi vil i dette eksempel kigge nærmere på billardkuglers elastiske stød.
To kugler med samme hastighed og samme masse bevæger sig direkte mod hinanden. Begge kugler har en hastighed på 2 m/s. Lad os opskrive dette som vektorer:
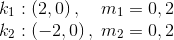

De to vektorer er her repræsenteret i et koordinatsystem. Begge kugler bevæger sig langs x-aksen men i modsat retning. Øverst har vi kuglerne der nærmer sig hinanden, og nederst har vi kuglerne lige efter stødet, hvor deres hastighedsvektorer har skriftet retning.
Altså vi lader de to kugler bevæge sig langs x-aksen. Når de rammer hinanden i et elastisk stød, bliver de begge skudt tilbage, og altså må deres vektorer vende 180 grader. Der er impulsbevarelse:
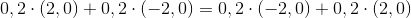
Vi får 0 på begge sider af lighedstegnet, og altså er impulsen bevaret.
Eksempel 2
Lad os nu forestille os at vi tager kuglen på 0,5 kg og sender den ud i rummet med en fart på 400 m/s. Ude i rummet møder den en meteor som trækker kuglen ind så den går i kredsløb omkring meteoren.
Kuglen ligger i kredsløb omkring meteoren 100 meter fra dens centrum og har stadig samme hastighed.
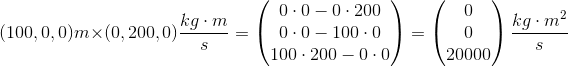
Impulsmoment står altså op vinkelret på både positionsvektoren og impuls vektoren og har en værdi på z-aksen på 20000 kg·m2/s hvilket er standart enheden for impulsmoment.

