Tyngdeacceleration
Tyngdeacceleration er den acceleration, som legemer får, når de påvirkes af tyngdekraften. Jordens tyngdekraft tiltrækker legemer ved at accelerere dem ind mod jordens massecentrum. Denne acceleration er ligesom tyngdekraften næsten konstant over hele jorden.
Tyngdeacceleration er også den samme for alle legemer uafhængigt af form eller masse.
Tyngdekraften derimod afhænger af massen på et legeme. Jo højere masse desto højere kraft virker på legemet. Men for at accelerere et legeme, skal man bruge en kraft, som er proportional med legemets masse. Dette betyder i sidste ende, at legemer med høj masse og legemer med lav masse falder med samme acceleration og vil dermed have samme hastighed, hvis de falder fra samme punkt.
Det var Isaac Newton der for første gang definerede tyngdekraften matematisk med følgende formel:
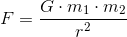
Gravitation
Dette kaldes også den universelle gravitations lov. Her er G den såkaldte universelle gravitationskonstant, m1 og m2 er masserne på de to legemer der tiltrækker hinanden, og r er afstanden (radius) i mellem dem. F er kraften.
I den Newton'ske mekanik trækker alle legemer med masse i hinanden med en kraft. Denne kraft kaldes gravitation. Det betyder at man i kraft af sin egen masse trækker i sin kollega/ven/nabo, men at han/hun samtidig trækker i dig med en ligeså stor kraft.
Gravitation er en kraft, der er meget svag. Man mærker derfor ikke noget til disse gravitations-krafter, hverken indbyrdes mellem mennesker eller med alle de ting, som vi omgiver os med. Gravitationen er så svag en kraft, at den acceleration den giver os eller ting omkring os, er umærkelig.
Jorden derimod har en ufattelig stor masse. Gravitationen mellem Jorden og de ting, der befinder sig i dens nærhed, er derfor væsentlig. Således er gravitationen skyld i at vi ikke blive "smidt af", under jordens rotation om sig selv.
Som en konsekvens af gravitationen fra Jorden, er alle legemer med masse i dens nærhed påvirket af en kraft rettet ind mod Jordens centrum. De vil derfor accelerere. Den acceleration, som gravitationen fra Jorden giver anledening til kaldes tyngdeaccelerationen.
Når man sætter jordens masse ind som den ene masse i formlen ovenfor og lader radius være jordens radius, får man kraften på overfladen. Når man regner denne som acceleration, får man jordens tyngdeacceleration. Denne kan man i de fleste praktiske tilfælde behandle som en konstant. I Danmark er tyngdeacceleration på 9,82 m/s2.
Hvis man skal regne meget præcist skal man have flere decimaler, og man skal regne med hvor på kloden man befinder sig. Jorden er er ikke en perfekt kugle men en ellipsoid, altså en fladmast kugle. Derfor vil vi have højere tyngde på polerne end på ækvator.
Når man har at gøre med et frit fald, kan man altså udregne et legemes hastighed ved at gange antal sekunder efter starten af faldet med tyngdeacceleration:
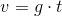
v er hastigheden i meter per sekund, g er tyngdeacceleration og t er tiden i sekunder.
Ud fra denne kan vi også udregne den strækning, man falder i frit fald. Formlen for strækning ser således ud:
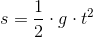
s er strækningen i meter, og igen er g tyngdeacceleration og t tiden.
Eksempel
Vi vil i dette eksempel regne på den acceleration, et legeme opnår ved at blive kastet fra rundetårn. Vi bruger standart tyngdeacceleration i Danmark på 9,82 m/s2. Vi lader legemet være en mønt. Som sagt kunne det være en hvilken som helst genstand, det ændrer ikke på regnestykket.
Rundetårn er 41,55 meter højt. Vi sætter strækningen 41,55 meter ind i vores formel og isolerer tiden:
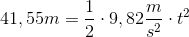

Altså vi ganger med 2 og dividerer tyngdeacceleration over på den anden side af lighedstegnet og tager kvadratroden for at fjerne den anden potens på tiden.
Nu ved vi, at det tager 2,91 sekund for mønten at nå jorden. Vi kan finde hastigheden med hastighedsformlen:
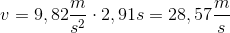
1 meter per sekund er lig 3,6 kilometer i timen, og altså får mønten en hastighed på:
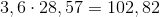
Mønten ender altså med en hastighed på 102,82 kilometer i timen, lige før den rammer jorden.

