Terning

En terning er en figur i rumgeometri. Terninger har seks sider, som alle er kvadrater. Det vil sige at en terning har samme højde, bredde og længde.

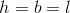
En terning minder om en anden rumgeometrisk figur, nemlig en kasse. Men de adskiller sig ved at kun terningen har kvadratiske sider.

Rumfang af en terning

Derfor er det også meget simpelt at beregne rumfang af en terning. Det gøres ved følgende formel:

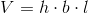
Terning.

Du kan se et eksempel på beregning af rumfang af en terning nederst.

Overfladeareal af terning

Overfladearealet af en terning er summen af arealet af alle terningens sider. Da alle siderne består af kvadrater, og de alle har samme størrelse, er overfladearealet nemt at regne ud. Vi behøver kun at kende sidelængden, så kan vi beregne kvadraternes areal, som er lig sidelængden i anden potens. Når vi har arealet behøver vi bare at gange med sideantallet, som er lig seks.

Terning med sidelængden (l) markeret.

Vi har altså følgende formel for overfladeareal af terning:

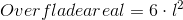
Eksempel

Vi udregner rumfang af en terning og derefter overfladearealet af en terning.

Terning med en sidelængde på 8 cm.

Når alle siderne pr. definition er lige store, kan man nemt beregne rumfang af en terning, hvor :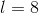

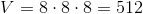
Dermed er rumfanget af denne terning målt i cm lig med 512 .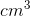

Vi indsætter sidelængden på 8 cm i vores formel for overfladeareal af terning:

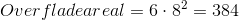
Vores terning har dermed et overfladeareal på 384 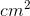.