Matematik
Løsning af differentialligning
Hej jeg skal finde ud af kuglens hastighed i beton og løsningen til differentialligningen
De tre kræfter der påvirker kuglen er:
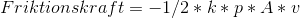 (Det skal lige sige at p er rho (ρ)
(Det skal lige sige at p er rho (ρ)
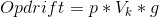
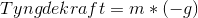
Den resulterende kraft er så Fres = Ft + Fop + FD
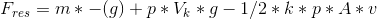
Vi finder acceleration vha. 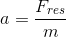
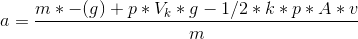
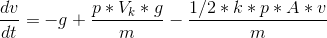
Hvis det ikke er helt rigtigt må i lige sige til. Men jeg tror dette er differentialligningen for kuglens bevælgelse i beton. Jeg skal herefter løse differentialligningen, som jeg ikke helt ved hvordan det skal gøres.
Kuglens masse : V * ρkugle og kuglens rumfang: 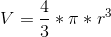 og kuglenstværsnit areal:
og kuglenstværsnit areal: 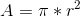
Min læreres endelig løsning er:
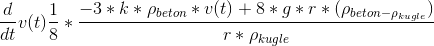
Hvordan kommer jeg fra min differentialligning til dette? hjælp
Svar #1
16. februar 2017 af UchihaItachi
Spørgsmålet i opgaven lyder: Angiv alle de kræfter der påvirker kuglen nede i betonen under hensyntagen til opdrift og friktion. Opstil Newtons 2. lov for kuglens lodrette bevægelse, og udled herfra en 1. ordens differentialligning i kuglens lodrette hastighed v(t) til beskrivelse af kuglens lodrette bevægelse i betonen.
Skriv et svar til: Løsning af differentialligning
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







