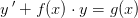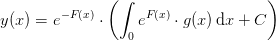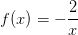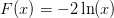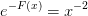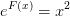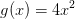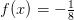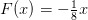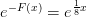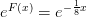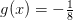Lige nu 311 online.

Persondatapolitik

Matematik

Den fuldstændige og partikulære løsning på en differentialligning.

17. februar 2017 af CelineHoppe (Slettet) - Niveau: A-niveau

Hej.
Jeg sidder med to opgaver som jeg har en del problemer med at løse:
Den ene opgave er: y´=2/x*y+4x^2

Hvor den fuldstændige og partikulære løsning skal findes, og at grafen går igennem punktet (1,2)

Den anden er dy/dx=1/8*y-0,125

Hvor den fuldstændige løsning og den partikulære løsning skal findes og samtidigt opfylder at y(6)=5.

Er der evt nogle der kan være behjælpelige med dem her?

Mvh en frustreret student.

Brugbart svar (0)

Svar #1
17. februar 2017 af mathon

Brug "panserformlen":

$y{\, }'+f(x)\cdot y=g(x)$

$y(x)=e^{-F(x)}\cdot \left (\int_0 e^{F(x)}\cdot g(x)\, \mathrm{d}x+C \right )$

Brugbart svar (0)

Svar #2
17. februar 2017 af mathon

i den første
med:
$f(x)=-\frac{2}{x}$ $F(x)=-2\ln(x)$ $e^{-F(x)}=x^{-2}$ $e^{F(x)}=x^{2}$ g(x)=4x^2

Brugbart svar (0)

Svar #3
17. februar 2017 af mathon

i den anden
med:
$f(x)=-\tfrac{1}{8}$ $F(x)=-\tfrac{1}{8}x$ $e^{-F(x)}=e^{\frac{1}{8}x}$ $e^{F(x)}=e^{-\frac{1}{8}x}$ $g(x)=-\tfrac{1}{8}$

Skriv et svar til: Den fuldstændige og partikulære løsning på en differentialligning.

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.

Seneste indlæg
9: Dansk Eksamen Mundtlige (0)
9: Kortfilm - eksamen (2)
9: Hvad giver 3a*b (1)
9: valg af underemne til 9. klasse ... (1)
9: ungdomssind som fordybbelsesområ... (1)

Populære indlæg
9: Dansk Eksamen Mundtlige (0)
9: Kortfilm - eksamen (2)
9: Kortfilm til eksamen (2)
9: Hvad giver 3a*b (1)
9: valg af underemne til 9. klasse ... (1)

Om Studieportalen.dk: Om Studieportalen.dk | Kontakt | Annoncering | Studiebladet | Ophavsret | Cookie- og persondatapolitik

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se