Matematik
Integration af ikke-differentiable funktioner
Hej derude
Jeg har lagt mærke til, at der i bøger står, at kravet for, at en funktion kan integreres er, at den skal være kontinuert. Der står dog intet om differentiabilitet, så jeg tænkte på, om I har nogle eksempler på funktioner, der differentieret giver en kontinuert, ikke-differentiabel funktion?
Jeg overvejede, om man kunne tage det ubestemte integral af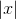 
i forhold til x og tænker umiddelbart, at man så vil få en funktion, der er voksende fra ![]-\infty;0]](https://media.studieportalen.dk/images/equations/B6N371Pe8FhnKM4R62ZymA==.gif)
, samt at dens graf "flader ud" i dette interval, indtil en vendetangent i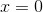 
nås, og herefter er funktionen voksende igen fra 
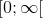(med voksende tangenthældning). Dette synes muligt, men vil denne funktion så ikke have en tangenthældning, der er både voksende og aftagende i ?
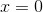Så alt i alt - er det muligt, at en funktion, der er differentiabel, giver en ikke-differentiabel, kontinuert funktion, når den differentieres?
Svar #1
18. juni 2017 af peter lind
En differentiabel funktion er kontinuert og dermed har den også en stamfunktion.
En funktion som den du nævner er kontinuert og har derfor en stamfunktion for eks -x2 for x<=0 og +x2 for x>0
Den funktion du nævner er ikke differentiabel i 0. Differenskoefficienen (f(0+h) -f(0))/h = |h|/h = -1 for h <0 og +1 for h>0
Svar #2
18. juni 2017 af SuneChr
# 0 Den første sætning, påstand, er ikke korrekt.
En ikke-kontinuert funktion kan f.eks. være en trappefunktion defineret i [a ; b]
En trappefunktion er konstant på det indre af ethvert delinterval af a = x0 < x1 < ... < xn = b
og er integrabel, uden at være kontinuert.
Svar #3
19. juni 2017 af Number42
Så længe som man kan finde arealet under "kurven" er den integrabel (måske med forskellige metoder).
Du kan ikke integrere en funktion som |x| fra -uendelig til noget som helst. Den funktion er ikke integrabel i det interval. Men fint fra a til b hvis hverken a eller b er uendelige (plus eller minus)
Differentieres 1/2 x^2 bliver det x og - 1/2 x^2 bliver til -x
Stanfunktionen du leder efter ser sådan ud (som vedhæftet):
Skriv et svar til: Integration af ikke-differentiable funktioner
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.