Lige nu 85 online.

Persondatapolitik

Studieportalen.dk › Kompendier › Fysik › Mekanik › Archimedes' lov

Archimedes' lov

Archimedes' lov beskriver, hvad der sker, når man sænker et objekt ned i en væske.

Archimedes lov siger, at når når et legeme sænkes ned i en væske, vil det få en kraft opad lig massen af den væske, den forskyder, når den sænkes ned.

Det er dette princip, der bestemmer, om legemer flyder eller synker i væsker.

Archimedes var en græsk matematiker og fysiker fra omkring 300 år før vores tidsregning.

Opdrift

Opdrift er den kraft, som skubber opad, når et legeme sænkes ned i en væske. Opdrift har altså den modsatte retning af tyngdekraften.

Opdrift findes i alle stoffer, der er derfor også opdrift i gasser ligesom i væsker.

Opdriftens kraft på et legeme er lig den tyngdekraften, legemet ville være udsat for, hvis det bestod af det samme som væsken.

Altså hvis vi sænker et jernlod ned i noget vand, er jernloddets opdrift lig tyngdekraften på det volumen vand, som blev skubbet væk, da loddet blev sænket ned.

For at finde denne tyngdekraft skal vi gange volumen med vands densitet og gange dette med tyngdeacceleration.

Vi kan skrive dette som en generel formel:

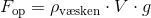
$F_{\text{op}} = \rho_{\text{v\ae sken}} \cdot V \cdot g$

Det første symbol, som ligner et p, er det græske bogstav rho. Rho er symbolet for massefylde. Massefylde kaldes også for densitet. Densitet er hvor meget, et bestemt stof vejer i forhold til sin volumen.

V er volumen af det legeme, der sænkes ned i vandet. Man kan også sige, at V er volumen af det vand, der bliver skubbet væk af det nedsænkede legeme.

g er tyngdeaccelerationen. Standardværdien for tyngdeaccelerationen er 9,82 m/s². Se artiklen Tyngdeacceleration.

Vi skal altså, for at finde et legemes opdrift, bruge væskens densitet, gange det med legemets volumen og gange dette med tyngdeacceleration.

Vi vil nu kigge på det mest almindelige eksempel på opdrift; når væsken er vand.

Opdrift i vand

Opdrift i vand er ikke kun det vigtigste eksempel på opdrift, det er også det mest simple.

Det skyldes blandt andet, at vands volumen og masse er forbundet med det simple forhold: 1 liter vand vejer 1 kg.

Det vil sige, hvis et objekt forskyder vand 1 liter, har det forskudt det 1 kg.

Vi kalder dette forhold for mellem vægt og størrelse for vands densitet, som altså er på 1 kg/Liter. Man kan også angive densiteten som 1 g/cm³.

Lad os se på et eksempel på opdrift i vand. Vi sænker et objekt ned i vand.

Et objekt sænkes i vand. Tyngdekraften og opdriften er illustreret med deres retning. Objektet skubber vandet til et højere niveau.

Det første, vi kan observere, er, om objektet sænker eller flyder, når vi giver slip på det. Det vil komme an på forholdet mellem tyngdekraften og opdriften.

Hvis tyngdekraften er højere end opdriften, vil objektet synke, og hvis opdriften er højere, vil det flyde.

Man kan også sige dette på en anden måde, hvis vi lader F_samlet være lig den samlede kraft af de to kræfter F_tyn og F_op:

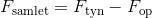
$F_{\text{samlet}} = F_{\text{tyn}} - F_{\text{op}}$

Da opdrift virker i den modsatte retning i forhold til tyngdekraften, skal opdriften trækkes fra. Så hvis den samlede kraft er positiv, synker objektet, og hvis den er negativ, flyder det.

Vi vil nu se på et konkret eksempel. En kugle af jern sænkes ned i vand. Kuglen har en volumen på 10 cm³ og en vægt på 78 gram. Vi beregner opdriften ved hjælp af vores formel.

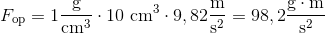
$F_{\text{op}} = 1 \frac{\text{g}}{\text{cm}^3} \cdot 10 \text{ cm}^3 \cdot 9,82 \frac{\text{m}}{\text{s}^2} = 98,2 \frac{\text{g} \cdot \text{m}}{\text{s}^2}$

Vi får enheden gram meter over sekund i anden. Vi vil omregne dette til standardenheden for kraft, hvilket er Newton. Newton er lig kg·m/s², så vi skal bare dividere vores resultat med 1000 for at gå fra g til kg.

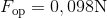
$F_{\text{op}} = 0,098 \text{N}$

Jernkuglen får altså en opdrift på 0,098 Newton fra vandet. Lad os også beregne tyngdekraften så vi har den samlede kraft.

Tyngdekraften udregnes med denne simple formel:

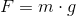
$F = m \cdot g$

F er kraften målt i Newton. m er legemets masse i kg, og g er tyngdeacceleration.

Tyngdekraften på jernkuglen er altså:

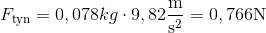
$F_{\text{tyn}} = 0,078 kg \cdot 9,82 \frac{\text{m}}{\text{s}^2} = 0,766 \text{N}$

Det giver os en samlet kraft på:

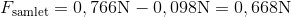
$F_{\text{samlet}} = 0,766 \text{N} - 0,098 \text{N} = 0,668 \text{N}$

Jernkuglen vil altså synke, da tyngdekraften er stærkere end opdriften.

Opdrift i luft

Opdrift i luft virker efter samme principper som i vand.

Vi vil finde opdriften af en to liters ballon fyldt med helium, i luften. For at gøre regnestykket mere simpelt antager vi, at selve ballonen er vægtløs, så vi kun skal regne på gassen.

Opdriften beregnes med vores formel, men i stedet for at have væskens densitet, skal vi for gasser bruge gassens densitet. Atmosfærens luft har en densitet på 0,0012 kg per liter ved havoverfladen.

Vi sætter ind i formlen:

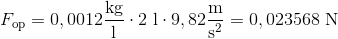
$F_{\text{op}} = 0,0012 \frac{\text{kg}}{\text{l}} \cdot 2 \text{ l} \cdot 9,82 \frac{\text{m}}{\text{s}^2} = 0,023568 \text{ N}$

For at finde ud af den samlede kraft der vil virke på gassen, skal vi også beregne dens tyngdekraft.

Først beregner vi vægten på de 2 liter helium. Helium har en massefylde eller densitet ved rumtemperatur på 0,0002 kg/l. Altså vægten af heliumgassen er 0,0004 kg.

Det kan vi sætte ind i formlen for tyngdekraft:

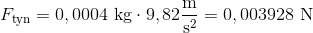
$F_{\text{tyn}} = 0,0004 \text{ kg} \cdot 9,82 \frac{\text{m}}{\text{s}^2} = 0,003928 \text{ N}$

Det giver en samlet kraft på:

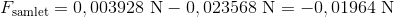
$F_{\text{samlet}} = 0,003928 \text{ N} - 0,023568 \text{ N} = -0,01964 \text{ N}$

Vi har en negativ samlet kraft, altså opdriften er højere end tyngdekraften, derfor vil helium gassen stige op i luften.

Seneste indlæg
A: Differentation (1)
A: Integral arealberegning for punk... (5)
9: Prøveoplæg til fordybelsesområde... (1)
Biostatistik og Epidemiologi i m... (0)
9: Jorden og Livets udvikling (0)

Populære indlæg
A: Differentation (1)
A: Integral arealberegning for punk... (5)
9: Levende reklamer (3)
9: hvorfor er kobber giftigt og sta... (4)
9: Prøveoplæg til fordybelsesområde... (1)

Hjælp: Support | FAQ | Stopplagiat.nu

Se også: Studienet.dk | Studienett.no | Studienet.se