Tyngdekraft
Tyngdekraft er den fysiske naturkraft, der får legemer til at tiltrække hinanden. Det er tyngdekraften, der gør, at vi bliver holdt fast til jordens overflade.
Hvad er tyngdekraft
Vi ved alle, at hvis vi lader en ting falde, vil den falde mod jorden. Dette skyldes, at jorden har en tyngdekraft, som virker på alting omkring den.
Tyngdekraften trækker altid i mod sig selv, og derfor falder vi altid mod jordens overflade.
Alle legemer med en masse udsættes for tyngdekraft og udgiver tyngdekraft.
Jo højere masse et legeme har, desto højere tyngdekraft giver det.
Det er derfor på grund af jordens høje masse i forhold til os, at vi bliver tiltrækket af jorden og ikke omvendt.
Det er også jordens tyngdekraft, som får månen til at kredse om jorden, ligesom det er solens tyngdekraft, som får jorden til at kredse om solen.
Som sagt giver alle legemer tyngdekraft, men her på jorden er der ikke nogen objekter, der har nok masse til at give en synlig tiltrækning.
Så selvom to fodbolde lagt ved siden af hinanden, i princippet er tiltrukket hinanden på grund af tyngdekraften, er kraften så svag, at den ikke har nogen betydning.
Ude i universet kan vi dog se tyngdekraftens effekt tydeligt, i den måde himmellegemerne bevæger sig. Måner kredser om planeter, fordi planeterne har højere masse.
Hvis der ikke var nogen tyngdekraft, ville månen bare flyve lige forbi planeten, men tyngdekraften bliver ved med at bøje månens bane ind mod planeten, så den ender med at cirkle omkring planeten.
De fleste himmellegemers baner i solsystemet er dog ikke cirkelformede men ellipseformede, fordi de på samme tid bliver tiltrukket af flere forskellige legemer og derfor får bøjet deres baner i forskellige retninger.
På samme måde som måner kredser om planeter, kredser planeter om stjerner. Stjernerne kredser om et massecentrum i deres galakse. Ofte har galakser et sort hul i midten, som får stjernerne til at kredse omkring sig. Selv galakser bevæger sig omkring et centrum i deres galaksehop, og galaksehope bevæger sig i en superhob.
Det samme princip gentager sig altså på flere skalaer i universet. Tyngdekraften former universet, uden den ville det ikke se ud, som det gør.
Gravitation
Gravitation er det samme som tyngdekraft. Gravitation kommer af det latinske ord 'gravis', som betyder tung, ordet blev lavet af Isaac Newton.
Ofte vil man bruge gravitation som det generelle navn for naturkraften, der tiltrækker massive legemer, og tyngdekraften som den specifikke kraft jorden har på os.
Gravitation blev først beskrevet af Isaac Newton og er helt grundlæggende for at forstå klassisk mekanik.
Gravitation virker ud fra tre parametre: Massen af de ene legeme, massen af det andet legeme og afstanden i mellem dem.
Hvis der er en forskel i masse mellem to legemer, vil det tungeste tiltrække det andet legeme.
Jo længere afstand mellem to legemer, desto svagere virker tyngdekraften.
Det betyder omvendt også, at jo tættere de er på hinanden, desto stærkere virker kraften. Altså vil to legemer, der trækkes mod hinanden, accelerere, så de bevæger sig hurtigere og hurtigere mod hinanden.
Gravitationskraft er en kraft, som kommer af gravitation. Gravitationskraft fortæller os det potentiale, gravitationen har for at accelerere legemer.
Selvom tyngdekraften føles meget stærk på her på jorden, er gravitation faktisk den svageste af de fire naturkræfter. Til gengæld virker den over langt større afstande end den stærke og svage kernekraft.
Einsteins relativitetsteori beskrev gravitation, ikke som en kraft der får objekter til at tiltrække hinanden, men som en bøjning af selve rummet. I relativitetsteorien er masse og energi det samme, og gravitation er en generel effekt, der får rummet til at bøje sig om enhver form for energi.
Denne måde at se gravitation på forklarer, hvorfor vi kan observere, at lys bliver bøjet i rummet over store afstande, den såkaldte gravitationslinseeffekt. Den klassiske måde at se gravitation på tillader ikke, at den kan bøje lys, fordi fotoner ikke har en masse.
Tyngdekraft formel
Der findes en generel tyngdekraft formel, som kommer fra Newtons love. Den beskriver gravitation ud fra de tre variable m1, m2 og r, og den såkaldte gravitationskonstant G:
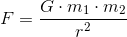
m1 og m2 er masserne af de to legemer, man regner på, og r er afstanden mellem dem.
r beregnes som afstanden mellem legemernes massecentrum. For planeter og stjerner er massecentrum i den indre kerne. Altså er afstanden ikke fra overflade til overflade, men fra centrumpunkt til centrumpunkt.
Bemærk også at afstanden r er i anden potens, hvilket i praksis betyder, at kraften vil falde hurtigere og hurtigere, når afstanden bliver længere.
G er gravitationskonstanten, som er lig 6,67428·10-11 N· m2/kg2.
F er selve kraften, som måles i Newton.
Med denne formel kan man beregne gravitationen mellem ethvert par af objekter. Vi vil nu gennemgå to konkrete eksempler: jordens og månens tyngdekraft.
Tyngdekraft på jorden
Vi vil beregne tyngdekraften på jorden, hvilket betyder, at vi vil finde ud af, hvor meget et legeme accelereres mod jordens centrum, når det befinder sig på overfladen.
Dette kaldes tyngdeaccelerationen. Se artiklen Tyngdeacceleration.
Vi beregner tyngdeaccelerationen med gravitations formlen:
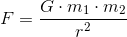
Vi lader m1 være jordens masse. m2 er massen på det legeme, der udsættes for tyngdekraften. m2 betyder ikke noget for selve accelerationen, så den kan vi fjerne. r er afstanden, og da vi befinder os på jordens overflade, skal den være jordens radius.
Jordens masse er 5,97·1024 kg, og radius omkring ækvator er 6378135 meter. Vi sætter ind i formlen:
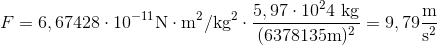
Jorden har altså en tyngdeaccelerationen på 9,79 meter per sekund i anden omkring ækvator. Det betyder, hvis man lader noget falde mod jorden, vil dets hastighed stige med 9,79 meter per sekund hvert sekund.
Jorden er ikke perfekt kugleformet, den er en smule fladmast, så ækvator har en længere radius end polerne. Derfor er tyngdeaccelerationen ikke den samme overalt på jorden.
Vi får derfor ikke helt den samme tyngdeaccelerationen som standardværdien på 9,82 m/s2, som bruger en gennemsnitsradius.
For at få tyngdekraften i Newton på et bestemt objekt skal vi gange tyngdeaccelerationen med massen af objektet.
Tyngdekraft på månen
Tyngdekraften på månen beregnes på samme måde som for jorden, og igen er det tyngdeacceleration, vi beregner.
Månen har en masse på 7,349·1022 kg og en radius på 1737300 meter.
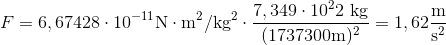
Månen har dermed en tyngdeacceleration på 1,62 m/s2. Dette betyder, at det vil føles som om, man er lettere på månen. Altså ca. 6 gange lettere.

