Matematik
Talmængders størrelse
Hvor stor er mængden af rationelle tal i forhold til mængden af irrationelle talt?
jeg har googlet løs men kan ikke finde noget om det.
mængden af hele tal må være dobbelt så stor som mængden af naturlige tal, hvad er forholdet mellem de andre talmængder?
Svar #1
29. september 2016 af Therk
Uha, du bevæger dig ind på et meget spændende område inden for matematik: Kardinalitet.
Det kan vises at mængden af naturlige tal er lige så stor som mængden af hele tal. Det kan også vises at mængden af rationelle tal er lige så stor som mængden af naturlige tal! Vi siger at de mængder er tællelige. Men det gælder ikke for de reelle tal! Dem er der nemlig utælleligt mange af - der er endda utælleligt mange flere relle tal mellem 0 og 1 end der er naturlige tal.
Vi skriver gerne:
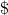
\# \mathbb Q = \# \mathbb N \stackrel{\text{def}}= \aleph_0 < \# \mathbb R \stackrel{\text{def}}=c
Og det læses:
Antallet af rationelle tal er lig antallet af naturlige tal, som vi definerer som "aleph nul". Det er en mængde, der er strengt mindre end antallet af reelle tal, som vi definerer som c.
Jeg kan henvise dig til den fremragende WIkipediaside om kardinalitet, og en Youtube-video, som Numberphile har lavet.
Svar #2
29. september 2016 af Capion1
Man kan vise, at mængden af rationale tal Q kan tælles, hvilket betyder, at der findes en en-entydig afbildning af Q på N , de naturlige tal.
Det er endvidere kendt, at mængden af de reelle tal R ikke kan tælles.
Da R udgør mængden af de rationale tal plus mængden af de irrationale tal I , har vi
R = Q ∪ I som viser, at I er utællelig.
Svar #3
09. oktober 2016 af RuneTrold (Slettet)
Hej igen
Tak for jeres svar! noget af det forstår jeg dog ikke endnu.. er kun nået til A-niveau.
Nu har jeg tænkt en masse igen og kan ikke rigtig komme videre.
Det jeg mente med at mængden af hel tal er dobbelt så stor som mængden af naturlige tal er vel rigtigt? eller deler man de to mængder op? Er de naturlige tal ikke en delmængde af mængden af heltal, or dermed dobbelt så stor? eller er det bare besluttet anderledes?
Nå. tilbage til det spændende.
Mængden af rationelle tal kan, som jeg forstår det, kun tælles i kraft af at man lister dem op i 2 dimensioner. For som han siger i numberphile, kan de ikke tælles hvis de listes i en dimension som en tallinje.
Kan man heller ikke liste/tælle de irationale og reelle tal, hvis man gør det i 3 dimensioner? eller flere?
Svar #4
10. oktober 2016 af Therk
Betragt et "simpelt" scenarie.
Hilbert ejer et meget specielt hotel: Der er uendeligt mange værelser på hotellet. Det betyder at han meget sjældent har problemer med at have værelser til rådighed. I tilfælde af at der er fuldt booket, og der kommer en ny gæst ville en normal hotelejer være nødt til at afvise gæsten. For Hilbert kan han blot bede alle gæster om at flytte til det næste værelse - da bliver værelse nummer 1 ledigt, mens alle andre stadig har et værelse.
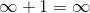
Nu sker der så det at der ankommer en bus med et usædvanligt fodboldhold: De er uendeligt mange spillere på holdet. Nu er Hilbert lidt presset, fordi hans hotel er jo fuldt booket. Men han klarer det alligevel: Han beder hver gæst om at flytte til værelset med det dobbelte værelsesnummer: Gæst i værelse 1 flytter til værelse 2, gæst i værelse 2 flytter til værelse 4 osv. Det betyder at alle de ulige værelser nu er ledige og fodboldholdet indlogeres i de ulige værelser.
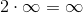
Du kan nu, ved hjælp af ovenstående analogi, måske overbevises om at antallet af lige tal er det samme som antallet af naturlige tal, selvom din intuition fortæller dig at der må være dobbelt så mange naturlige tal som lige tal - "vi har jo ikke medtaget den anden halvdel: De ulige!"
Generelt er to mængder af samme størrelse, hvis man kan skabe en "en-til-en" afbilding mellem de to mængder. Lad os prøve det med de hele tal:
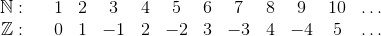
Som du kan se kan vi liste tallene i en logisk rækkefølge (husk at vi aldrig stopper med listen!). De to mængder er dermed lige store, og vi kalder dem tælleligt uendelige.

Problemet med de relle tal er at uanset hvordan vi prøver at gribe det an, så eksisterer der ikke et "næste tal". Og så er det lige meget hvor mange dimensioner vi har at arbejde i; vi kan kun indsætte ét tal, vores "første" tal. Vi kommer aldrig videre derfra.
Svar #5
10. oktober 2016 af RuneTrold (Slettet)
Hvad hvis der flytter en ud af Hilberts hotel, vil der så også stadig være uendeligt mange tilbage? eller 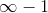 ?
?
Eller hvis der flytter uendeligt mange ud vil der vel være 0 tilbage? lige gyldigt hvor mange gange der er flyttet uendeligt mange ind.
Mængden af 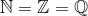 selvom
selvom 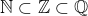 ? Eller er det misfrostået med
? Eller er det misfrostået med 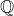 ?
?
Man kan ikke argumentere for at mængden af rationale tal er 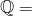
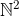 eller
eller 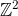 da der skal to dimensioner til før de kan tælles?
da der skal to dimensioner til før de kan tælles?
Har stadig svært ved at se de irrationale ikke kan tælles. Men det falder nok først på plads når jeg når på universitet. Der er vel lavet en masse beviser for det :)
Svar #6
10. oktober 2016 af VandalS
Kardinalitet er noget af en hjernevrider, selv med en baggrund i videregående matematik. Ofte er ens intuition ikke i overensstemmelse med matematikken fordi begrebet "uendelig" er sådan en mærkelig størrelse. Hvis du lægger til, trækker fra, ganger eller dividerer 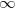 med endelige tal er resultatet stadig
med endelige tal er resultatet stadig 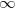 , så sammenligninger som "dobbelt så stor", "mindre end" osv. giver ikke længere mening.
, så sammenligninger som "dobbelt så stor", "mindre end" osv. giver ikke længere mening.
Den klasse af 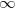 som Therk giver eksempler på i #4 (tælleligt uendelig) kaldes
som Therk giver eksempler på i #4 (tælleligt uendelig) kaldes 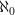 , og en lang række af uendeligheder viser sig at tilhøre denne klasse - f.eks alle lige tal, alle ulige tal,
, og en lang række af uendeligheder viser sig at tilhøre denne klasse - f.eks alle lige tal, alle ulige tal, 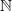 ,
, 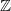 og mange flere. Alligevel findes der typer af uendeligheder der er "større" end
og mange flere. Alligevel findes der typer af uendeligheder der er "større" end 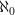 ; mængden af reelle tal er et eksempel herpå, da de reelle tal ikke er tællelige. Det er stadig et åbent spørgsmål om hvorvidt mængden af reelle tal tilhører
; mængden af reelle tal er et eksempel herpå, da de reelle tal ikke er tællelige. Det er stadig et åbent spørgsmål om hvorvidt mængden af reelle tal tilhører 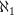 eller befinder sig et sted imellem
eller befinder sig et sted imellem 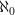 og
og 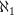 (kendt som kontiniuums hypotesen).
(kendt som kontiniuums hypotesen).
Du kan måske have gavn af at læse https://en.wikipedia.org/wiki/Aleph_number hvor nogle klasser af uendeligheder (og eksempler herpå) gennemgås.
Svar #7
10. oktober 2016 af VandalS
Tillæg til #6:
De almindelige regnearter bryder også sammen hvis du forsøger at bruge dem på uendelige størrelser, da resultatet af udregningerne kan afhænge af fortolkning.
For at sætte det på spidsen kan du forestille dig et fuldt booket Hilberts hotel. Der starter med at være 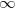 mange gæster. Hvis du smider alle gæsterne i værelser med et lige nummer ud forsvinder der
mange gæster. Hvis du smider alle gæsterne i værelser med et lige nummer ud forsvinder der 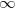 gæster, men der er stadig
gæster, men der er stadig 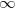 mange tilbage. Hvis du derimod smider alle gæsterne ud fjerner du også
mange tilbage. Hvis du derimod smider alle gæsterne ud fjerner du også 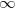 mange gæster, men der er nu 0 tilbage. Regnemæssige udtryk som
mange gæster, men der er nu 0 tilbage. Regnemæssige udtryk som  giver derfor ikke god matematisk mening, så man skal udvise stor forsigtighed i argumenter der involverer uendelige størrelser.
giver derfor ikke god matematisk mening, så man skal udvise stor forsigtighed i argumenter der involverer uendelige størrelser.
Svar #8
10. oktober 2016 af Therk
Du har allerede set et bevis på at de reelle tal er utællelige - de giver dig det, godt nok ikke formelt, men heuristisk i Youtube-videoen. Det supersimple bevis kaldes Cantors diagonalargument.
Jeg undgik med vilje at lade gæster flytte ud af hotellet igen i mit eksempel, da det begynder at blive noget vrøvl, hvis der flytter for mange ud, som du selv bemærker og som VandalS fint beskriver - vi støder netop ind i problemet med at et udtryk ikke har et entydigt svar.
Det er ikke korrekt at 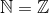 , da
, da  ("-1 er i Z, men ikke i N") - de to mængder er bestemt ikke ens! Vi benævner kardinalitet som "#S", som betyder "antal elementer i S". Da de naturlige og de hele tal har samme antal elementer, men har færre elementer end de reelle tal, skriver vi derfor
("-1 er i Z, men ikke i N") - de to mængder er bestemt ikke ens! Vi benævner kardinalitet som "#S", som betyder "antal elementer i S". Da de naturlige og de hele tal har samme antal elementer, men har færre elementer end de reelle tal, skriver vi derfor
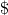
Svar #9
10. oktober 2016 af RuneTrold (Slettet)
Nej. men antallet er elementer i mængderne eller mængdernes størrelser er vel ens, men det giver vel næsten sig selv for de naturlige og heltallene 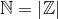 . Jeg kan godt se at det jeg skrev var helt forkert skrevet, der manglede ligesom noget. :)
. Jeg kan godt se at det jeg skrev var helt forkert skrevet, der manglede ligesom noget. :)
og med hensyn til diagonal argumentet tænkte jeg at man "bare" kunne lægge en dimension eller flere til, og dermed gøre de irrationelle tal tællelige. (ligesom man gjorde for at gøre de rationale tal tællelige.) ved trække en diagonal på en eller anden led igennem det talrum af reelle tal der måtte opstå.
Grunden til mit spørgsmål i første omgang (forholdet mellem mængden af rationale og irrationale tal) var at hvis de var lige store, kunne man gange 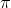 , e eller et hvilket som helst andet irrationalt tal med et rationalt tal or dermed skrive de andre irrationale tal. Jeg fandt kort efter ud af det det overhodet ikke forholder sig sådan! Det kørte så der ud af, for svar avler spørgsmål.
, e eller et hvilket som helst andet irrationalt tal med et rationalt tal or dermed skrive de andre irrationale tal. Jeg fandt kort efter ud af det det overhodet ikke forholder sig sådan! Det kørte så der ud af, for svar avler spørgsmål.
I skal have mange tak for jeres svar! Jeg har bestemt lært en masse nyt, men lige nu er jeg lidt overvældet, der har været meget ny information. Så nu vil jeg gå tilbage til at regne på kugler og planer, det er langt mere håndgribeligt. :)
Svar #10
10. oktober 2016 af Capion1
Ja, Alice (i Eventyrland) undrede sig også over mærkværdigheder, uendeligheden, evigheden, ja, relativitetsfænomener, selv om de slet ikke var "opfundet" på hendes tid.

Svar #11
10. oktober 2016 af Jegvedingenting
#1
Spændende video, især den sidste del.
Så, konklusionen er at "uendelige" størrelser alligevel er "begrænsede" i en eller anden forstand?
Skriv et svar til: Talmængders størrelse
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.







