Matematik

Hjælp!

18. oktober 2019 af OleJensenv - Niveau: B-niveau

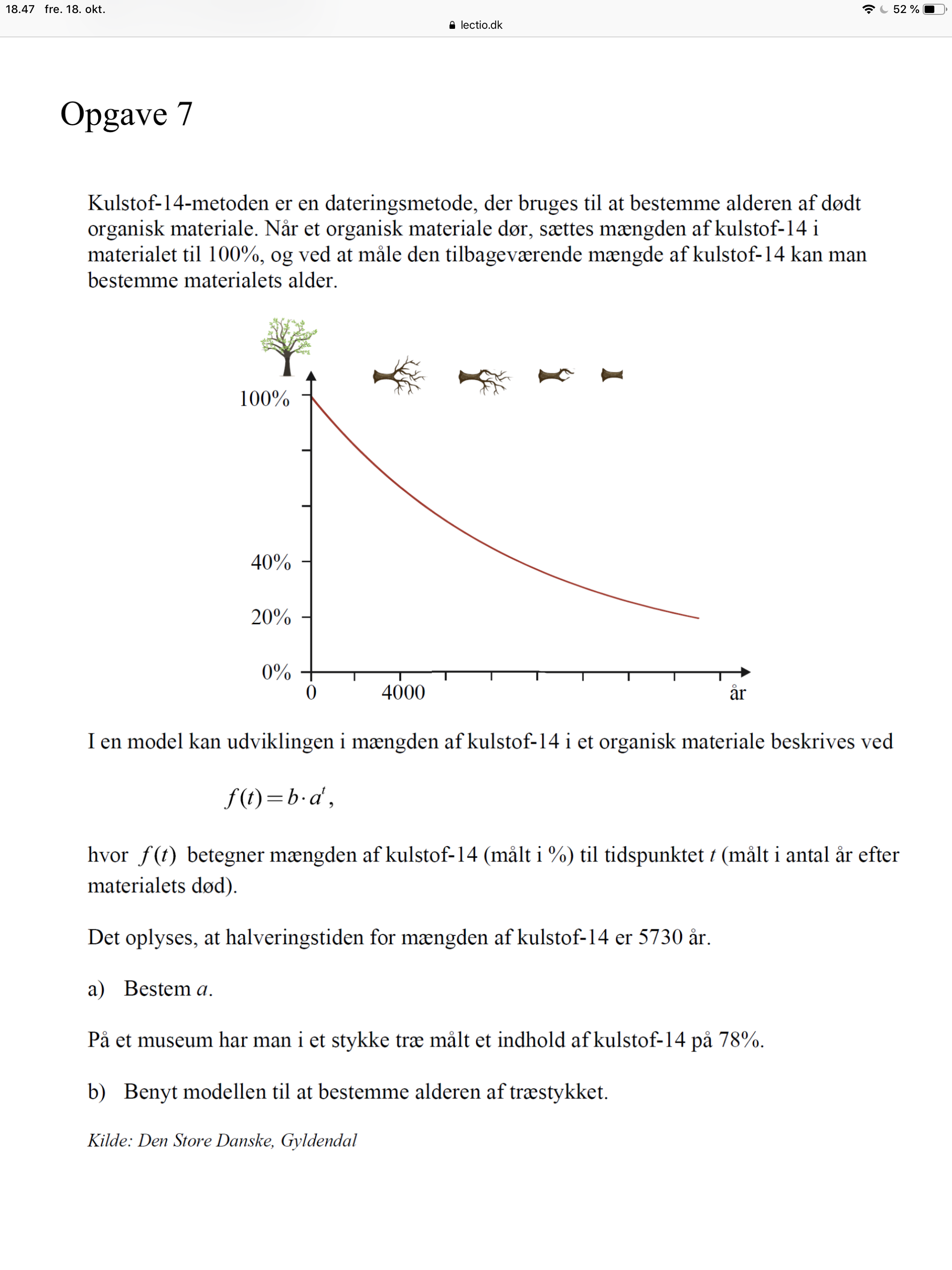
Hej jeg er gået lidt i stå i denne opgave, tror at jeg skal benytte mig af formlen for halveringstiden - dog ikke sikker.
Tak på forhånd.

Vedhæftet fil: 9224606F-99FC-4EDF-9BA2-8D2DA19162A6.png

Brugbart svar (0)

Svar #1
18. oktober 2019 af mathon

Brugbart svar (2)

Svar #2
18. oktober 2019 af mathon

$\small \small \small \small \begin{array}{lllllll} a)&\textup{t er antal d\o ds\aa år og f(t) = tilbagev\ae rende }^{14}C\\\\ &f(t)=100\cdot a^t\\\\ &\frac{50}{100}=a^{5730-0}\\\\ &a=\left (\frac{1}{2} \right )^{\frac{1}{5730}}=0.999879\\\\ b)&f(t)=100\cdot 0.999879^t=78\\\\ &0.999879^x=0.78\\\\ &\log(0.999879)\cdot t=\log(0.78)\\\\ &t=\frac{\log(0.78)}{\log(0.999879)} \end{array}$

Brugbart svar (0)

Svar #3
18. oktober 2019 af ringstedLC

Det er en god ide:

$\begin{align*} T_{\frac{1}{2}} &= \frac{\log (\frac{1}{2})}{\log (a)} \end{align*}$

Svar #4
18. oktober 2019 af OleJensenv

Du er en helt #2

Svar #5
18. oktober 2019 af OleJensenv

Hvad mener du #3? Det er jo formlen for halveringstiden.

Brugbart svar (1)

Svar #6
18. oktober 2019 af ringstedLC

Ja, fordi:

$\begin{align*} 5730 &= \frac{\log\left ( \frac{1}{2} \right )}{\log (a)} \\ a &= \log^{-1}\left ( \frac{\log\left ( \frac{1}{2} \right )}{5730} \right ) \\ &= 0.999879 \end{align*}$

Brugbart svar (0)

Svar #7
18. oktober 2019 af AMelev

Du får opgivet både variable størrelser, forskrift og to sæt sammenhørende værdier af (t,f(t)), (0,100) og (5730,50) (da de 100% er halveret til 50% efter 5730 år).

a) Benyt (102) & (103) s. 19 i din formelsamling. Det er måske lidt nemmere. Du kan også benyte, at du ved, at b = f(0), så b = 100.

b) Opstil forskriften for f og løs ligningen f(t) = 78.

Brug dit CAS-værrktøj og tjek på graf.

Brugbart svar (0)

Svar #8
19. oktober 2019 af mathon

$\small \begin{array}{llllll} \textup{CAS-kontrol:}&\textup{solve}\left ( 100\cdot\left (\left ( \frac{1}{2} \right )^{\frac{1}{5730}} \right )^x =90,x \right ) \end{array}$

Skriv et svar til: Hjælp!

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.