Halveringstid
Halveringstid er inden for fysik et mål for, hvor hurtigt et radioaktivt materiale henfalder.
Halveringstiden er den gennemsnitlige tid, det tager, før halvdelen af et materiales atomer er henfaldet. Man kan altså, ved at undersøge forskellige radioaktive isotoper eksperimentelt, tilknytte en halveringstid til disse.
Man betegner halveringstiden med symbolet T½. Efter et tidsforløb, t, kan man udregne, hvor meget der er tilbage af den originale mængde, N0, af et ustabilt stof.
Vi har denne halveringstidsformel eller -funktion:
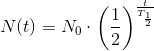
N(t) er mængden af stof til tiden t, N0 er mængden vi starter med, og T½ er halveringstiden. Hvis t er lig T½, vil vi altså få halvdelen af N0 tilbage. Hvis t er lig to gange T½, vil vi få en fjerdedel af N0 tilbage og så videre.
Halveringstid hænger tæt sammen med den såkaldte henfaldskonstant k, da:
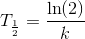
Jo længere halveringstid et stof har, desto svagere er dets radioaktivitet. Der findes radioaktive stoffer, som har så lang halveringstid, at de næsten kan betragtes som stabile.
Eksempel
Vi har i et laboratorium fundet en isotop med en halveringstid på 2 dage. Vi har 500 milligram af dette stoffet, og vil udregne hvor meget der er tilbage efter 10 dage.
Vi bruger vores halveringstid formel:
Efter 10 dage er der altså kun 15,63 milligram tilbage af isotopen.


