Tryk
Tryk er i fysik et mål for, hvor meget pres en overflade bliver udsat for. Tryk er dermed kraft per areal. For eksempel er standardenheden newton per kvadratmeter. Denne enhed kaldes også Pascal. Standardenheden newton per kvadratmeter er også lig kilogram over meter gange sekund i anden.
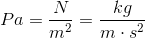
En anden af de forskellige trykenheder, der ofte bruges er bar, som er dekanewton per kvadratcentimeter, hvilket vil sige at en bar er lig 100 000 Pascal.
Man regner på tryk i mange forskellige sammenhænge som for eksempel meteorologi. Jordens atmosfære giver et tryk overalt på dens overflade. Da det er næsten det samme over hele jorden, har vi en standardenhed kaldet atmosfære, som er lig med 101325 Pascal. Vi vil i denne artikel regne på tryk i væske og tryk i gas.
Tryk i væskesøjle
Trykket i en væskesøjle i en bestemt dybde, er lig summen af af væskesøjlens og luftens (atmosfærens) tryk. Hvis vi har en sø og går h meter ned, har vi altså en væskesøjle med højden h, som presser ned på alt i denne dybde.
Tryk i vand.
På figuren er søjlen illustreret. Ud over søjlens tryk har vi også luftens tryk som vi kalder p0. Trykket man bliver udsat for på denne dybde, kommer an på densiteten af væsken. Altså hvor tung væsken er. Hvis vi for eksempel var i et hav af kviksølv, ville trykket være langt større end i et hav af vand.
Det tryk væsken giver skyldes jo tyngdekraften, som trækker alt ind mod jordens centrum. Derfor skal vi gange væskesøjlens masse med tyngdeaccelerationen g. Altså må trykket være lig densiteten ρ gange højden h gange tyngdekraften g, plus luftens tryk p0.
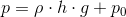
Se eksempel 1, for hvordan vi bruger denne formel til at udregne trykket af en væskesøjle.
Tryk i gas
Selvom gas er lettere end væsker har de stadig et tryk. I en gas er partiklerne meget mindre end den afstand de har til hinanden, så de skaber ikke ikke noget indbyrdes tryk på hinanden som i væsker. Gas partikler bevæger sig mere eller mindre tilfældigt rundt i mellem hinanden, men udfylder hele det rum de bevæger sig i.
Den hastighed gaspartikler bevæger sig med, kommer an på gassens temperatur. Jo højere temperatur jo højere hastighed. Da tryk er et mål for presset på en en overflade, vil en gas med højere temperatur have højere tryk, da partiklerne rammer overfladen med højere hastighed.
Tryk i gas.
Da gaspartikler er så meget mindre end afstanden de har til hinanden, betyder det ikke noget hvilke partikler gassen består af, men kun deres temperatur og mængden af dem. Trykket af en gas kan beregnes ved den såkaldte idealgaslov.
Idealgasloven
Idealgasloven ser på en formel således ud:
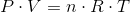
P er gassens tryk i pascal
V er gassens volumen i kubikmeter
n er stofmængden i mol
R er idealgaskonstanten 8,3145 J/(mol·K)
T er gassens temperatur i kelvin
Man ganger altså mængden af partikler med temperaturen og med idealgaskonstanten for at få trykket over hele volumen. Hvis man bare vil have trykket, skal man dermed bare dividere med V på hver side af lighedstegnet. Enheden mol er standart enheden for at måle antal partikler. En mol er 6,022110 · 1023.
Se i eksempel 2 hvordan man bruger idealgasloven til at beregne tryk af en gas.
Eksempel 1
Når en dykker svømmer ned på 20 meters dybde, hvilket tryk bliver han så udsat for? Vi kan svare på dette spørgsmål ved at bruge formlen for tryk af væskesøjle.
Vi har højden som er 20 meter, og vi har p0 som er 101325 Pascal (1 atmosfære), da vandet jo bliver udsat for atmosfærens tryk. Tyngdeaccelerationen g er lig 9,81 m/s2 og densiteten ρ af vand er 1000 kg/m3.
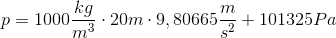
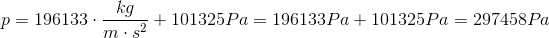
Pascal er kilogram over meter gange sekund i anden. Så vores enheder passer, og vi får et tryk på 297458 Pascal. Hvis vi dividerer dette med atmosfæretrykket, får vi hvor mange atmosfæres tryk dykkeren bliver udsat for.
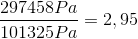
En dykker, der svømmer 20 meter ned i havet vil altså opleve et tryk på 2,95 atmosfære, et næsten tre gange højere tryk end på land.
Eksempel 2
Vi har 1 mol gas i en kasse på 1 kubikmeter. Inde i kassen er temperatur 20 grader celsius. Vi skal omregne celsius til Kelvin for at enhederne passer i idealgasligningen. Kelvin er lig celsius plus 273,15.
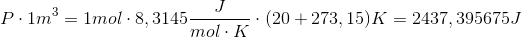
Vi bruger nu at vi kan omskrive Joule til Newton gange meter:
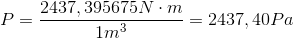
Gassen i denne kasse giver altså et tryk på 2437,40 Pascal, omkring 2 % af atmosfærens tryk.



