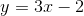Sekant
En sekant er et linjestykke, der går mellem to punkter, primært på en kurve. Men en sekant kan også være et linjestykke mellem to punkter på en cirkelperiferi. Denne artikel beskæftiger sig primært med en sekant til en graf af en funktion.
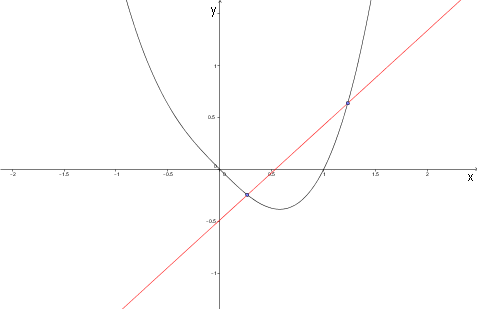
Sekant (den røde linje) mellem to punkter på en kurve.
En sekant kan tegnes på en hvilken som helst kurve eller graf. Ofte bruger man sekanter i forbindelse med cirkler, hvor enhver linje der går igennem cirkelperiferien to steder, er en sekant.
Sekanter til en graf af en funktion siger noget om hvordan grafen stiger og falder.
Derfor er sekanter meget brugt i differentialregning, hvor man bruger dem til at finde differenskvotienter. En differenskvotient er hældningen af en sekant. Når man har fundet differenskvotienten, lader man afstanden mellem sekantens to punkter gå mod nul, for at finde differentialkvotienten.
En sekant defineres af de to punkter, hvor den skærer grafen. Hvis vi kalder de to punkter p og q, har vi koordinaterne:
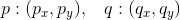
Med koordinaterne kan vi finde sekantens ligning. En sekants ligning er bare linjens ligning, 
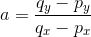
Når vi har hældningen kan vi indsætte et af punkterne i sekantens ligning og finde b.
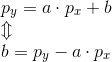
Vi har nu ligning for en sekant.
Eksempel
Vi vil nu finde hældningen på en sekant.
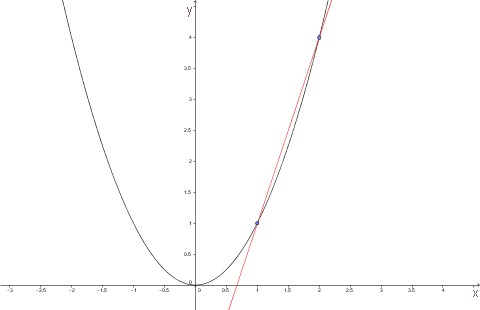
Kurve med sekant (rød).
Kurven er grafen for funktionen f(x):
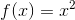
De to punkter, p og q, har koordinaterne:
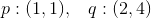
Se også afsnittet 'linjens ligning ud fra to punkter' i artiklen Linjens ligning.
Vi beregner hældningen:
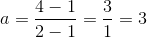
Nu kan vi finde b:
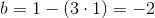
Vores sekant har altså ligningen: