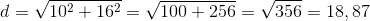Rektangel
Et rektangel er en firkant, altså indenfor geometrien(plan) en figur med fire sider. Et rektangel er karakteriseret ved at de 4 hjørner alle skal være vinkelrette (90 grader), og at de modstående sider er parallelle og parvis lige lange.
Et rektangel minder derfor om et parallelogram hvor de modstående sider også er parvis lige lange, men i et rektangel er vinklerne samtidigt rette, det gælder ikke et parallelogram. Et rektangel adskiller sig samtidig fra et kvadrat, hvor alle fire sider er lige lange.
Rektangel med diagonaler.
Linjerne fra D til B og A til C er rektangelets diagonaler. En diagonal er en linje mellem modstående hjørner. De to diagonaler vil i et rektangel altid være lige lange, og de halverer altid hinaden præcis midt på. Diagonalerne har også den egenskab, at de deler et rektangel op i to retvinklede trekanter.
Areal af rektangel
Arealet af et rektangel udregnes ved at gange de to sider med hinanden. Medmindre alle sider er lige lange (da vil rektanglet samtidig være et kvadrat), vil et rektangel have to lange sider og to korte sider. Derfor kalder vi ofte de to sidelængder for højden (h) og bredden (b).
Højden og bredden af et rektangel.
Det giver os en formel for et rektangels areal:
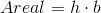
Da et rektangel per definition er todimensionelt kan man ikke tale om et rektangels rumfang, da rumfanget er den tredimensionelle version af areal. Derfor kan rumfang kun udregnes for tredimensionelle figurer (se kapitlet der handler om rumgeometri).
Omkreds af rektangel
Omkredsen af et rektangel udregnes ved at finde summen af alle sidelængderne. Siderne består af de to parallelle par, hvis længde definerer højden og bredden af rektanglet, så omkreds må være lig det dobbelte af højden plus bredden:
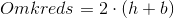
Diagonal i rektangel
En diagonal deler et rektangel ind i to retvinklede trekanter.
Diagonal i rektangel med længde d.
For at finde diagonallængden, d, skal vi betragte rektangelet som to trekanter. Hvis vi kender højden og bredden af rektangelet kender vi dermed også to af siderne (de to kateter i en retvinklet trekant) i trekanterne. Den sidste side (hypotenusen i en retvinklet trekant) er diagonalen. Denne kan vi udregne ved hjælp af Pythagoras sætning. Pythagoras sætning siger at:
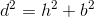
Så d kan findes ved at tage kvadratroden på begge sider af lighedstegnet. Det vil sige at diagonalen i rektanglet er:
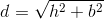
Eksempel
I dette eksempel har vi et rektangel med højden 10 og bredden 16.
Eksempel på rektangel med h = 10 og b = 16.
Beregn areal af rektangelet:
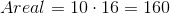
Beregn omkredsen:
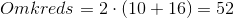
Og til sidst kan vi beregne rektangelets diagonal længde: