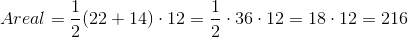Areal af trapez
Areal af trapez beregnes ud fra højden og den gennemsnitlige længde af de to parallelle sider.
For at udregne arealet af et trapez har vi altså brug for at finde højden. Højden er længden af et linjestykke, der går vinkelret fra den ene af de parallelle linjer til den anden.
Trapez med højde
Hvis man ikke kan tegne højden direkte, fordi den ene side er kortere end den anden, kan man udvide den ene side i samme retning, indtil man kan tegne højde-linjen. Se eksempel 3.
For at få det korrekte areal skal vi bruge gennemsnittet af længden af de 2 parallelle sider. Det får vi ved at lægge de to længder sammen og tage halvdelen af dette resultat. Dette gennemsnit skal vi gange med højden for at få arealet. Altså har vi denne formel for areal af et trapez:
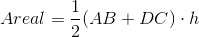
Man kan IKKE beregne rumfang af trapez. Et trapez er en figur i to dimensioner, og derfor har den ikke noget rumfang. Trapezer tegnes i planen, og derfor kan man med andre ord kun beregne areal af trapez.
Vi vil nu beregne arealet af forskellige trapezer.
Eksempel 1
Det første eksempel har vi et trapez, hvor den øverste og nederste linje er parallelle.
Eksempel på trapez.
Den øverste linje har en længde på 14 cm og den nederste 11 cm. Højden er målt til 12 cm.
Vi sætter længderne ind i areal formlen:
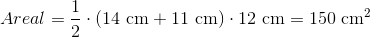
Dette trapez har dermed et areal på 150 cm2.
Eksempel 2
Vi vil i dette eksempel beregne arealet på et ligebenet trapez.
Eksempel på et ligebenet trapez.
Dette trapez er opbygget af to parallelle linjer på 4 cm og 18 cm, og vi har en højde på 10 cm.
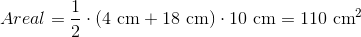
Det giver os et areal på 110 cm2 for dette ligebenede trapez.
Eksempel 3
Dette trapez har sine parallelle sider på hver side. Det betyder, at vi skal måle længden af højre og venstre side i stedet for den øverste og nederste side.
Eksempel 3 trapez med den ene side udvidet.
Dette trapez er dog lidt mere indviklet at finde højden på. Vi skal tegne en linje, højden, mellem de to parallelle skrå sider, som står vinkelret på begge sider. Da den ene side er langt kortere end den anden, bliver vi nødt til at udvide figuren for at kunne tegne højde.
Vi gør altså den korte side længere, og derefter tegner man en linje, vinkelret ud fra denne, op til den modsatte side. Det giver os den L-formede striplede linje på figuren.
Når vi har tegnet højden, måler vi den og får 10 cm. De to parallelle sider er henholdsvis 10 cm og 5 cm. Vi sætter ind i arealformlen:
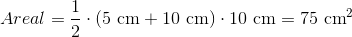
Trapezet har altså et areal på 75 cm2.
Eksempel 4
I dette eksempel kender vi de to parallelle siders længde og har målt højden.
Eksempel 4 trapez
Vi kan nu udregne arealet ved hjælp af vores formel:
