Trapez
Et trapez er en firkant, altså en figur indenfor geometri med fire sider. Det eneste vi kræver, for at kunne kalde en firkant et trapez, er at mindst to af siderne er parallelle.
Hvis de to andre sider også er parallelle, er dette trapez samtidig et parallelogram. Fordi et trapez har denne brede definition, vil en rombe, et kvadrat og et rektangel også være en form for trapez, og alle har de den egenskab at de fire vinkler i figuren lagt sammen giver 360 grader. Men betegnelsen trapez benyttes primært til figurer, der netop IKKE har de specifikke karakteristika som de øvrige figurer har.
Når et trapez har ét retvinklet hjørne, kalder vi det et retvinklet trapez. Grundet de to parallelle sider som definitionen af et trapez kræver, har et retvinklet trapez faktisk altid to vinkler på 90 grader.
Trapez.
Ligebenet trapez
Et ligebenet trapez er en speciel form for trapez, der har den egenskab at, udover at have to parallelle sider (AB og CD), er de to andre sider (AD og BC) lige lange.
Ligebenet trapez
Dette betyder at vinklerne i hver ende af de parallelle sider er lig med hinanden:
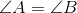
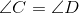
Et ligebenet trapez kan se ud som ovenstående. Havde de to lige lange sider (AD og BC) været parallelle, havde vi dermed haft et parallelogram.
Trapez formel
Man kan ikke tale om én decideret trapez-formel, men derimod findes der forskellige formler til at udregne et trapez' egenskaber. For eksempel kan man udregne højden af et trapez, hvis man kender én sidelængde og vinklen over denne. Formlen for højden vil så være sidelængden gange med sinus af vinklen:
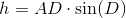
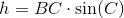
Generelt for et trapez skal vi kende alle sidelængderne for at udregne omkredsen, som er summen af disse. Det vil sige formlen for et trapez' omkreds er:
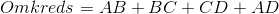
Hvis vi har et ligebenet trapez, som den ovenstående figur kan vi bare tage den dobbelte længde af BC og droppe det sidste led:
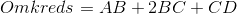
Man kalder de linjer man kan tegne mellem et trapez' hjørner for dets diagonaler.
Trapez med diagonalerne markeret som striplede linjer.
Man bruger højden til at udregne arealet af et trapez. Se artiklen Areal af trapez.
Eksempel 1
Vi vil i dette eksempel beregne højden på et trapez.
Eksempel trapez med en vinkel og en sidelængde givet.
Vi har givet et trapez, hvor vi kun kender en sidelængde og sidens vinkel øverst.
Vi beregner højden ved formlen:
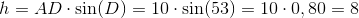
Denne trapez har dermed en højde (den striplede grå linje på figuren) på 8.





