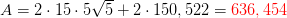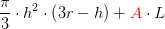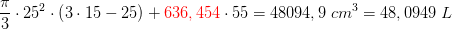Matematik
Spørgsmål om vand liter i beholder og parallelle linjer.
Mine komplikationer,
Jeg har to opgaver hvor jeg er rimelig lost.
Opgave c1)
Den første omhandler, at jeg har et vandret liggende beholder (i billede nedenunder kan man se det i snit), det er en cynlinder med en halvkugle for hver ende. Jeg har både udregnet rumfanget og det samlede overfladeareal (som var de forrige opgaver).
Nu skal jeg blot udregne det rumfang som vandet udgør i beholderen (det er i cm målene, så hvis jeg finder cm^3, vil jeg få det i ml, som jeg senere kan omregne.)
Vandets højde i beholderen er oplyst til at være 25 cm (h1). Men jeg aner ikke hvorledes jeg skal se på de/ udregne dett, så nogle hints ville være dejligt.
Opgave c2)
I denne opgave skal vi betsemme ligningen for den tangent til grafen f, som er parallel med funktionen g.
Funktionerne er givet ved, g(x)=-0.4 x+0.5 og f(x)=x+(e)^(-2 x)
Jeg ved så meget at de skal have den samme hældning for at være paralelle. Har blot problemer med at få ligningen til at ramme grafens f's minimumspunkt (hvor tangenthældningen er). Så gerne hjælp her også.
p.s man kan se graferne på nedenstående vedhæftning også.
Svar #1
31. august 2014 af mathon
Del rumfanget op i
To halvkugler dvs en kugle med radius 15 + en cylinder med længden 55 begge med
vandhøjden 25
Svar #3
31. august 2014 af mathon
fejl i #2 rettes når jeg får tid,. Tværsnitsarealet er forkert - det er noteret som et volumen.
Svar #4
02. september 2014 af mathon
Cylinderens tværsnitscirkel indlagt i et koordinatsystem med x-aksen som tangent og centrum på y-aksen
har ligningen
x2 + (y-15)2 = 152 -15 ≤ x ≤ 15 0 ≤ y ≤ 30
hvoraf
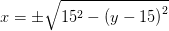
som med væksehøjden
y = 25
giver
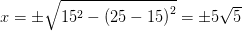
arealet af cylinderens væsketværsnit er således
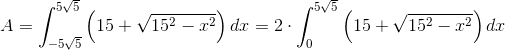
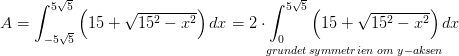
Svar #5
02. september 2014 af mathon
beregningen:
![A=2\cdot \int_{0}^{5\sqrt{5}}\left (15+\sqrt{15^2-x^2} \right )dx=2\cdot \left [ 15x \right ]_{0}^{5\sqrt{5}}+2\cdot \int_{0}^{5\sqrt{5}}\sqrt{15^2-x^2}dx=](https://media.studieportalen.dk/images/equations/QxOAzDbASIGyWc-aPrjp4Q==.gif)
hvor beregningen
af
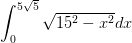 udføres ved substitutionen
udføres ved substitutionen
x = 15·sin(φ) og dermed dx=15·cos(φ)dφ
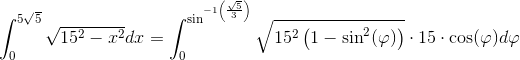
Svar #9
02. september 2014 af mathon
Opgave c2)
tekstredigering:
I denne opgave skal vi bestemme ligningen for den tangent til grafen for f(x), som er parallel med grafen for den lineære funktion funktion g(x)
dvs
I denne opgave skal vi bestemme ligningen for tangenten til grafen for f(x) i (1,f(1)).
Svar #11
03. september 2014 af mathon
detaljer i formlen for volumen af væsken i en kugle i højden h:
Indlæg en halvcirkel med centrum i (r,0) i 1. kvadrant
Denne har ligningen
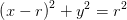
hvoraf
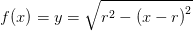
Med M begrænset af koordinatakserne, grafen for f(x) og linjen x = h med 0 < h < 2r
har man for en 360°'s drejning af M om x-aksen:
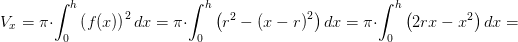
![\pi \cdot \left [ r\cdot x^2-\frac{1}{3}\cdot x^3 \right ]_{0}^{h}=\pi \cdot \left (r\cdot h^2-\frac{1}{3}\cdot h^3 \right )=\frac{\pi }{3}\cdot h^2\cdot \left ( 3r-h \right )](https://media.studieportalen.dk/images/equations/hrF__xdLXJ3SBKXanWAT6Q==.gif)
Skriv et svar til: Spørgsmål om vand liter i beholder og parallelle linjer.
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.




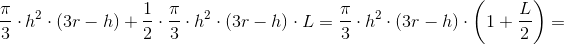
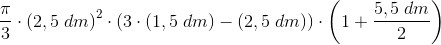
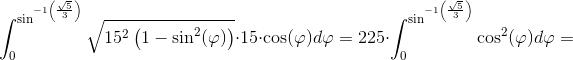
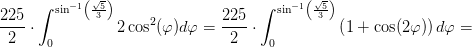
![\! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \! \frac{225}{2}\cdot \left [ \varphi +\frac{1}{2}\cdot \sin(2\varphi ) \right ]_{0}^{0,841069}=\frac{225}{2}\cdot \left ( 0,841069+\frac{1}{2}\cdot \sin(2\cdot 0,841069) \right )=150,522](https://media.studieportalen.dk/images/equations/hD7sugYnkpb8HQ43fByJvA==.gif)