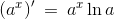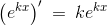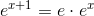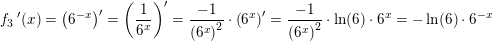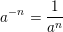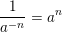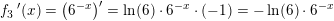Matematik

Find den afledede af nedenstående funktioner.. Hjælp..:-)

17. august 2017 af aliciaemilien - Niveau: B-niveau

Hej derude,

Jeg er i gang med en aflevering der omhandler regneregler for differentialkvotienter..
Jeg er gået lidt i stå med nogle af funktionerne. Det drejer sig om;

f₃(x)=6^-x

f₄(x)=1/2*e^-6x

f₆(x)= e^x+1

Opgaven lyder på at jeg skal finde den afledede af hver af funktionerne, men jeg er lidt i tvivl om hvordan. Indtil nu har jeg brugt denne oversigt; http://www.webmatematik.dk/lektioner/matematik-b/differentialregning/afledede-funktioner

jeg håber der er en der kan hjælpe mig, tak på forhånd :-)

Brugbart svar (1)

Svar #1
17. august 2017 af SuneChr

$\left ( a^{x} \right )'\: =\: a^{x}\ln a$

$\left ( e^{kx} \right )'\: =\: ke^{kx}$

$e^{x+1}=e\cdot e^{x}$

Brugbart svar (1)

Svar #2
17. august 2017 af mathon

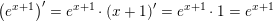$\small \left ( e^{x+1} \right ){}'=e^{x+1}\cdot \left ( x+1 \right ){}'=e^{x+1}\cdot 1=e^{x+1}$ _{differentieret som sammensat funktion}

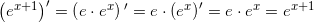$\small \left ( e^{x+1} \right ){}'=\left (e\cdot e^x \right ){ }'=e\cdot \left ( e^x \right ){}'=e\cdot e^x=e^{x+1}$ _{differentieret som konstant gange eksponentiel funktion}

Svar #3
17. august 2017 af aliciaemilien

#1
$\left ( a^{x} \right )'\: =\: a^{x}\ln a$

tak for svar, følger fortegnet med?

så vi ender (6^-x)' = 6^-x In 6 ? eller besvare man opgaven med det du har skrevet?

Brugbart svar (1)

Svar #4
17. august 2017 af mathon

$\small \small {f_3}{\, }'(x)=\left (6^{-x} \right ){}'=\left (\frac{1}{6^x} \right ){}'=\frac{-1}{\left ( 6^x \right )^2}\cdot \left ( 6^x \right ){}'=\frac{-1}{\left ( 6^x \right )^2}\cdot \ln(6)\cdot 6^x=-\ln(6)\cdot 6^{-x}$

Svar #5
17. august 2017 af aliciaemilien

#4
$\small \small {f_3}{\, }'(x)=\left (6^{-x} \right ){}'=\left (\frac{1}{6^x} \right ){}'=\frac{-1}{\left ( 6^x \right )^2}\cdot \left ( 6^x \right ){}'=\frac{-1}{\left ( 6^x \right )^2}\cdot \ln(6)\cdot 6^x=-\ln(6)\cdot 6^{-x}$

Taak, tror jeg forstår det nogenlunde, skal bare lige høre, hvor 1 kommer fra? :-)

Brugbart svar (0)

Svar #6
17. august 2017 af mathon

pr definition:
$\small a^{-n}=\frac{1}{a^n}$

hvoraf
$\small \frac{1}{a^{-n}}=a^n$

Svar #7
17. august 2017 af aliciaemilien

Kan jeg måske få dig til at sætte lidt ord på det? :-)

er -x så = n? og a = 6? :)

er ikke så skarp til det, men jeg vil rigtig gerne lærer, og forstå det, så jeg skal bare lieg være helt sikker.. :-)

Brugbart svar (0)

Svar #8
17. august 2017 af mathon

Ja.

Svar #9
17. august 2017 af aliciaemilien

takker :-)

Svar #10
17. august 2017 af aliciaemilien

#6
pr definition:
$\small a^{-n}=\frac{1}{a^n}$

hvoraf
$\small \frac{1}{a^{-n}}=a^n$

Jeg tror ikke helt jeg forstår hvorfor, at man skal bruge det her, kan du forklare det? :-)

Brugbart svar (1)

Svar #11
17. august 2017 af mathon

behøver du heller ikke:

$\small {f_3}{\, }'(x)=\left (6^{-x} \right ){}'=\ln(6)\cdot 6^{-x}\cdot (-1)=-\ln(6)\cdot 6^{-x}$

Svar #12
17. august 2017 af aliciaemilien

okaay :p

Skriv et svar til: Find den afledede af nedenstående funktioner.. Hjælp..:-)

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.