Matematik
u-substitution
Bestem konstanten k således at funktionen er en tæthedsfunktion
![g(x)=k\cdot f(x), for x\in [0,2]](https://media.studieportalen.dk/images/equations/zMVsRAcuS-II0ckyxbJ5Yg==.gif)
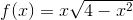
Jeg har svært ved at integrere funktionen f(x) ved brug u-substitutions metoden.
Jeg er gået i stå her:
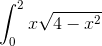
u er:
u = 4-x2
vi differentiere u og isolere du:
du/dx=-2x <=> du=-2x dx
Tak på forhånd
Svar #1
17. november 2014 af Soeffi
Du får
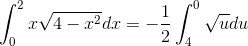
hvor u er det, som du er skrevet. x1=0 => u1=4 og x2=2 => u2=0.
Svar #2
17. november 2014 af Ibo199
hmm..hvor blev x af og hvordan kom du frem til at grænserne (4,0), det forstår jeg ikke helt?
Svar #4
17. november 2014 af Ibo199
Resten kan jeg godt forstå nu, men kan stadig ikke forstå hvordan grænserne lige pludselig bliver til (4,0). Kan jeg ikke få en forklaring?
Svar #5
18. november 2014 af Andersen11 (Slettet)
#4
Når x løber fra 0 til 2, løber u = 4 - x2 fra 4-02 = 4 til 4 - 22 = 0 .
Skriv et svar til: u-substitution
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


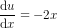 dvs
dvs 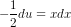
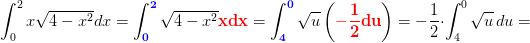
![\frac{1}{2}\int_{0}^{4}\sqrt{u}\, du=\frac{1}{2}\cdot \left [\frac{2}{3}u\sqrt{u} \right ]_{0}^{4}=\frac{1}{3}\cdot \left [ u\cdot \sqrt{u} \right ]_{0}^{4}=\frac{1}{3}\cdot \left ( 4\cdot 2-0\cdot \sqrt{0} \right )=\frac{8}{3}](https://media.studieportalen.dk/images/equations/5f_aPOHJgbYTQpd-riRBdg==.gif)