Matematik

Convergence

27. maj 2015 af Niko83 (Slettet) - Niveau: Universitet/Videregående

Hej derude.
Jeg har en opgave, der lyder:
Vis, at rækken

Vis, at rækken 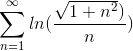$\sum_{n=1}^{\infty}ln(\frac{\sqrt{1+n^2})}{n})$

er konvergent, og dens sum er mindre end $\frac{\pi}{4}$

Hvis man tager grænserne til 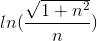$ln(\frac{\sqrt{1+n^2}}{n})$ , så konvergerer udtrykket mod ln(1) .
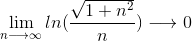or . $\lim_{n\longrightarrow \infty}ln(\frac{\sqrt{1+n^2}}{n})\longrightarrow0$ .

0 er mindre end fjerde del pi, men det lyder trivielt, så den ikke giver nogen mening.

Min spørgsmål er: Hvordan kan man viser, at dens sum er mindre end $\frac{\pi}{4}$ .

Jeg håber, at nogen er der ude for at hjælpe.
.

Brugbart svar (1)

Svar #1
28. maj 2015 af Drunkmunky

Vi betragter integralet

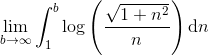
$\lim\limits_{b\rightarrow\infty}\int_{1}^{b}\log\left(\frac{\sqrt{1+n^{2}}}{n} \right )\text{d}n$

Ved brug af partiel integration med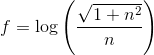 $f=\log\left(\frac{\sqrt{1+n^{2}}}{n} \right )$ og dg/dn=1. Så får vi, at

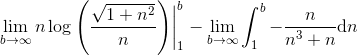$\lim\limits_{b\rightarrow\infty}n\log\left(\frac{\sqrt{1+n^{2}}}{n}\right)\biggr|_{1}^{b}-\lim\limits_{b\rightarrow\infty}\int_{1}^{b}-\frac{n}{n^{3}+n}\text{d}n$ .

Ved at indsætte b og 1 ind i det første led, får vi at det giver

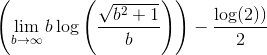
$\left(\lim\limits_{b\rightarrow\infty}b\log\left(\frac{\sqrt{b^{2}+1}}{b} \right ) \right )-\frac{\log(2))}{2}$

Hvor grænseværdien af første led er nul, så alt i alt har vi nu, at

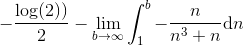
$-\frac{\log(2))}{2}-\lim\limits_{b\rightarrow\infty}\int_{1}^{b}-\frac{n}{n^{3}+n}\text{d}n$

Ved at trække minusset ud og dividere igennem med n i integralet, får vi, at

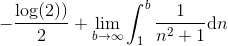
$-\frac{\log(2))}{2}+\lim\limits_{b\rightarrow\infty}\int_{1}^{b}\frac{1}{n^{2}+1}\text{d}n$

Det sidste integral har stamfunktion arctan(n), og da grænseværdien af arctan(b) når b går mod uendeligt er π/2 og arctan(1)=π/4, så får vi at integralet er lig med

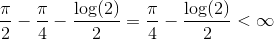
$\frac{\pi}{2}-\frac{\pi}{4}-\frac{\log(2)}{2}=\frac{\pi}{4}-\frac{\log(2)}{2}<\infty$

Så da integralet konvergerer, konvergerer rækken. Af dette følger det også at summen af rækken er mindre end π/4, da log(2)/2>0.

Svar #2
28. maj 2015 af Niko83 (Slettet)

Takkkkkkkkk, det er så venlig af dig

Skriv et svar til: Convergence

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.