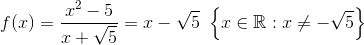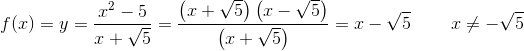Matematik
Forkorte brøker
Givet en funktion
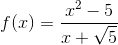
Hvis man tegner denne i matematikprogram får man en linje. Det er vel forkert. Jeg kan naturligvis se, at man kan faktorisere og forkorte væk for x ≠ -√5, men selv det passer ikke. For i omegnen af -√5 vil f(x) opføre sig ekstremt og være uendelig stor/uendelig lille afhængig af retning.
Hvordan kan man nogensinde forkorte brøker som disse under betingelsen at x ≠ -√5, så det er -√5 og dets omegn?
Svar #5
06. september 2016 af overkontroversiel
Det som I skriver er ret trivielt. Prøv nu at plotte grafen for
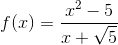 og
og 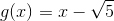 for x ≠ -√5
for x ≠ -√5
De vil opføre sig vildt forskelligt i omegnen x ≠ -√5. Grafen for f(x) vil efterligne opførslen af 1/x for x omkring 0 mens g(x) ikke er defineret i -√5.
Svar #6
06. september 2016 af Skaljeglavedinelektier
Jeg får nu begge grafer til at være meget ens. Faktisk helt ens.
Svar #7
06. september 2016 af overkontroversiel
Det er forkert. Din graftegner foretager selv den udregning (det er pointen i sidste ende), som #1 og #3 har vist. Prøv at bruge en tilnærmet værdi af √5 ≈ 2.236067977
Svar #8
06. september 2016 af Skaljeglavedinelektier
Jeg kan ikke se nogen forskel, men det kan være, dine øjne er bedre end mine.
Svar #9
06. september 2016 af mathias1997
Mener du sådan?
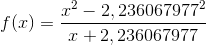
Det giver udmiddelbart det samme, nu er det bare den negativt tilnærmede værdi, der er udelukket fra definitionsmængden.
Svar #10
06. september 2016 af overkontroversiel
Det er lidt basic matematik. Prøv at lade x → ∞ og x → -∞
Svar #11
06. september 2016 af Skaljeglavedinelektier
Jeg er ikke helt med på, hvad du mener der i vejen med de to grafer, jeg har vedhæftet?
Jeg er ikke den bedste til de her graf programmer.
Svar #12
06. september 2016 af peter lind
#5 Tæt ved x = -kvrod(5) kan du ikke stole på hvad en CAS værktøj, lommeregner eller lignende leverer. Det skyldes afrundningsfejl
Svar #13
06. september 2016 af mathias1997
Jeg er med på, hvad du mener med, at funktionen burde opføre sig asymptotisk når 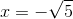
Det er også lidt et mysterium for mig.
Svar #14
06. september 2016 af Therk
Der sker ikke noget ekstremt nogen steder i din funktions definitionsmængde. Vores første indskydelse er normalt at se på funktionens afledte, hvis vi er interesserede i dens opførsel. Bemærk da at
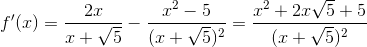
(forlæng den første brøk med sin nævner og reducer).
Du kan nu enten faktorisere tælleren eller forlænge nævneren. Uanset hvad, fremgår det nu at differentialkvotienten for funktionen er 1 for alle x.

Det stemmer naturligvis også overens med at grænseværdierne for funktionens afledte fra begge sider giver 1, modsat hvad din intuition fortæller dig. Hvis du har haft undervisning om grænseværdier, ved du muligvis at det tit kan hjælpe at omskrive udtrykket:
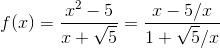
(vi bekymrer os ikke om division med 0, da ovenstående kun er interessant i den konfliktende grænseværdi. Nu kan vi lade x gå mod √5:
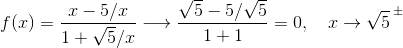
Da grænseværdierne er ens fra begge sider er det normalt at definere funktionens værdi i punktet til grænseværdien.

Slutteligt: Har du prøvet at plotte funktionen? Det burde gøre dig mistænkelig for hvad din intuition fortæller dig med "ekstrem opførsel".
Det ser da ikke så ekstremt ud.
Svar #15
06. september 2016 af overkontroversiel
Jeg har fundet ud af det nu.
Lige præcis, Therk. Jeg tog grænseværdien forkert og nej, jeg har ikke har haft undervisning i det endnu.
Skriv et svar til: Forkorte brøker
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.