Matematik

Differentialkvotient

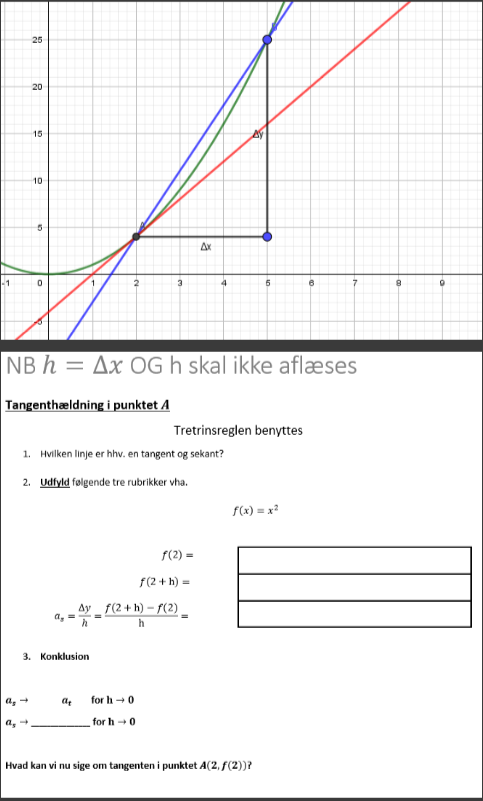
14. september 2018 af 8julihalvfems (Slettet) - Niveau: B-niveau

Jeg skal lave disse opgaver (Se billede)

Nr. 1 hvor jeg skal skrive hvilke linjer der er hhv. tangent og sekant, den har jeg styr på, men er total lost ved de andre. Jeg har læst og læst og kan bare ikke få det til at fise ind på lystavlen.

De tal jeg er kommet frem til i de 3 rubrikker er 4, 25 og 1 (første rubrik oppefra og ned). Og tror desværre jeg er helt på bar bund.

Håber der er nogle som kan hjælpe.

Vedhæftet fil: Unavngivet.png

Brugbart svar (0)

Svar #1
14. september 2018 af swpply (Slettet)

Brugbart svar (1)

Svar #2
14. september 2018 af swpply (Slettet)

Sekant blå

Tangent rød

$f(2) = 2^2 = 4$

$f(2+h) = (2+h)^2 = 2^2 + h^2 + 2\cdot2 h = h^2 + 4h + 4$

$\frac{f(2+h)-h(2)}{h} = \frac{h^2+4h + 4 - 4}{h} = h+4$

Altså kan du konkludere at $a_s \rightarrow 4$ for $h \rightarrow 0$ .

Tangenten i punktet A(2,f(2)) har dermed hældningskoefficient 4.

Svar #3
14. september 2018 af 8julihalvfems (Slettet)

#2
Sekant blå

Tangent rød

Altså kan du konkludere at for .

Tangenten i punktet A(2,f(2)) har dermed hældningskoefficient 4.

Jeg tror det lykkedes dig, at få mig til, at forstå det bedre. Dine tal virker ikke så rodede som dem jeg selv har siddet og læst på i vores bøger. Jeg takker mange gange og får skrevet nogle ordentlige noter ned som jeg kan forstå.

Skriv et svar til: Differentialkvotient

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.