Fysik

Inertimoment

08. juni 2020 af Mislaaa - Niveau: B-niveau

Hej alle, jeg arbejder med inertimoment af en kugle i fysik, og undrede mig egentlig lidt over hvordan man beregner det.

Jeg ved, at for en massiv kugle gælder:
I = 2/5 * m * R^2

og for en hul kugle, med en ubetydelige vægtykkelse gælder:
I = 2/3 * m * R^2

Jeg undrede mig derfor, hvis man nu har en kugle, som egentlig har en kugleskal på et par centimeter, om man så stadig beregner den som en hul kugle, eller om man egentlig burde tage udgangspunkt i den måske har en både indre og ydre radius? lidt ligesom hvordan man beregner for en hul cylinder (I = 1/2 * m * (R^2 + r^2), hvor man her tager udgangspunkt i den indre og ydre.

Jeg har prøvet at google det, men synes ikke jeg blev klogere, håber nogen kan gøre mig lidt klogere på dette!

Brugbart svar (1)

Svar #1
08. juni 2020 af peter lind

Du kan både beregne det som en hul kugle og svarende til en hul cylinder. Det sidste er det nemmest-

Udregn inertimomentet for en massiv kugle for de to radier og træk inertimimentet for den lille fra den stor

Svar #2
08. juni 2020 af Mislaaa

Mange tak! Det vil jeg prøve

Brugbart svar (0)

Svar #3
11. juni 2020 af Soeffi

#0. Formlen findes ikke, sikkert fordi den er for indviklet. Jeg har prøvet at udlede den baseret bl.a. på denne video, der handler om inertimomentet for en kugle. Ideen er at dele kuglen op i skiver vinkelret på z-aksen og integrere intertimomenterne af disse skiver. I beregningen indgår skivernes densitet = M/V, hvor M er legemets masse og V dets rumfang.

For en hul kugle med en indre radius på r og en ydre på R, så er man nød til at opdele legemet i to dele
I) To kalotter: een for oven og een for neden på kuglen.
II) En tøndelignende figur i midten.
Dette er vist nedenfor.

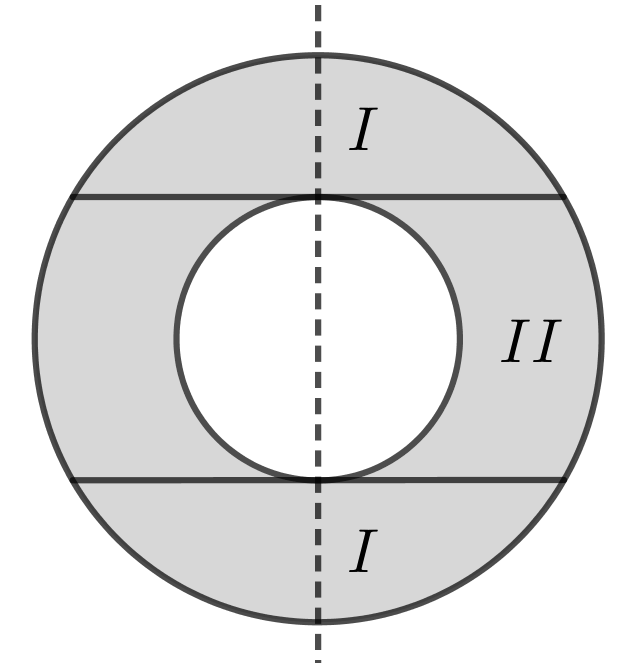
I) Rumfanget af de to kuglekalotter er: 2·(π/6)·(R-r)²·(6R-2(R-r)) = 2·(π/3)·(R-r)²·(2R+r)) =
II) Rumfanget af den tøndelignende figur er (4π/3)·R³ - (4π/3)·r³ - 2·(π/3)·(R-r)²·(2R+r) = 2·π·r·(R²-r²)

I) For kalotterne får man at

$dI_1= \frac{1}{2}\cdot x^2 \cdot dM= \frac{1}{2}\cdot x^2 \cdot \rho \cdot dV=\frac{1}{2}\cdot x^2 \cdot \rho \cdot (\pi \cdot x^2) \cdot dz=\frac{1}{2}\cdot \rho \cdot \pi \cdot x^4 \cdot dz=$

$\frac{1}{2}\cdot \frac{M}{V} \cdot \pi \cdot x^4 \cdot dz=\frac{1}{2}\cdot \frac{3M}{2\pi (R-r)^2\cdot (2R+r)} \cdot \pi \cdot x^4 \cdot dz=$

$\frac{3M}{4 (R-r)^2 (2R+r)} (R^2-z^2)^2 dz$

Dette integreres med hensyn til z fra r til R og ganges med 2:

$I_1=\frac{3 M}{4 (R-r)^2 (2 R+r)} \cdot 2 \int_{r}^{R}(R^2-z^2)^2 dz=$

$I_1=M\cdot \frac{8R^3+R^2r+6 R r^2-3r^3}{10 (2R+r)}$

Det bemærkes, at for r → 0 (en massiv kugle), så får man (2/5)·M·R², hvilket stemmer med formlen.

II) For den tøndelignende figur, så får man:

$dI_2= \frac{1}{2}\cdot (x_1^2+x_2^2) \cdot dM= \frac{1}{2}\cdot (x_1^2+x_2^2) \cdot \rho \cdot dV=$

$\frac{1}{2}\cdot (x_1^2+x_2^2) \cdot \rho \cdot (\pi \cdot (x_2^2-x_1^2)) \cdot dz=\frac{1}{2}\cdot \rho \cdot \pi \cdot (x_2^4-x_1^4) \cdot dz=$

$\frac{1}{2}\cdot \rho \cdot \pi \cdot ((R^2-z^2)^2-(r^2-z^2)^2) \cdot dz=$

$\frac{1}{2}\cdot \frac{M}{2\cdot \pi \cdot r\cdot (R^2-r^2)} \cdot \pi \cdot ((R^2-z^2)^2-(r^2-z^2)^2) \cdot dz=$

$\frac{M}{4 \cdot r\cdot (R^2-r^2)} \cdot ((R^2-z^2)^2-(r^2-z^2)^2) \cdot dz$

Dette integreres med hensyn til z fra 0 til r og ganges med 2:

$I_2=\frac{M}{4 \cdot r\cdot (R^2-r^2)} \cdot 2\int_{0}^{r}((R^2-z^2)^2-(r^2-z^2)^2) \cdot dz=$

$I_2=\frac{1}{2}(R^2+\frac{1}{3}r^2)\cdot M$

Det bemærkes, at denne formel går mod (2/3)·R²·M for r → R (en kugleskal), hvilket stemmer med formlen.

Tilsammen får man !₁ + I₂ =

$I= \frac{8\cdot R^3+R^2\cdot r+6 \cdot R \cdot r^2-3\cdot r^3}{10 \cdot (2\cdot R+r)}\cdot M_1+\frac{1}{2}\cdot (R^2+\frac{1}{3}\cdot r^2)\cdot M_2$

Man skal finde formlerne for de masseandelen af I) og II):

$M_1 = M\cdot \frac{(R-r)(2\cdot R+r)}{2\cdot (R^2+R\cdot r+r^2)}$

$M_2 = M\cdot \frac{3\cdot r\cdot (R+r)}{2\cdot (R^2+R\cdot r+r^2)}$

Samlet får man inertimomentet:

$I= \frac{2 \cdot R^4+2 \cdot R^3\cdot r+5\cdot R^2 \cdot r^2-R\cdot r^3+2\cdot r^4}{5 \cdot (R^2+R \cdot r+r^2)}\cdot M$

Vedhæftet fil:hulkugle.png

Skriv et svar til: Inertimoment

Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk? Klik her for at oprette en bruger.