Fysik
Dosishastighed
Hvordan bestemmer man den maksimale dosishastighed, en patient må udsættes for?
Svar #2
01. april 2021 af mathon
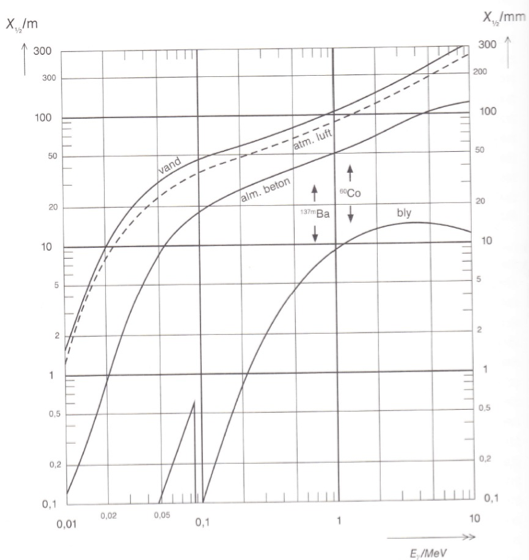
Du går ind på x-aksen under den pågældende energi af partiklen og op ad y aksen aflæser du på kurvem halveringstykkelsen
Svar #3
01. april 2021 af CecilieBebsi (Slettet)
Du går ind på x-aksen under den pågældende energi af partiklen og op ad y aksen aflæser du på kurvem halveringstykkelsen
Det er jeg ikke helt med på?
Svar #4
01. april 2021 af mathon
Henfaldsenergien er 1.17 MeV heraf patikelenergien (β-) 0.514 MeV
dvs
gammaenergien 0.656 MeV
Svar #7
01. april 2021 af mathon
b)
Lige omkring kilden er gammafaktoren 20.3 · 10-18 Sv·m2
I afstanden 2.0 m er den
Svar #8
01. april 2021 af mathon
b)
Lige omkring kilden er gammafaktoren 20.3 · 10-18 Sv·m2
I afstanden 2.0 m er den
Med
giver det
Svar #9
01. april 2021 af mathon
Denne skal nu dæmpes ved gennemgang af beton, hvis halveringstykkelse er ca. 40 mm.
Beregning af betontykkelse:
Svar #10
02. april 2021 af CecilieBebsi (Slettet)
#5
Hvor har du den formel fra? og hvorfor dividerer du med 0,30 (går ud fra det er de 30%)
Svar #12
02. april 2021 af CecilieBebsi (Slettet)
#11Du har ret.
Okay, men hvor kommer den formel fra?
Svar #14
03. april 2021 af CecilieBebsi (Slettet)
#13Dosishastighed er jo dosis per tid.
Okay, men hvorfor dividerer du den ækvivalente dosis patienten må modtage med de 30% personen har absorberet?
Svar #15
03. april 2021 af CecilieBebsi (Slettet)
#8b)
Lige omkring kilden er gammafaktoren 20.3 · 10-18 Sv·m2
I afstanden 2.0 m er den
Med
giver det
Hvorfor ganger du aktiviteten med 3600 h-1?
Svar #17
03. april 2021 af CecilieBebsi (Slettet)
#16...fordi enheden Bq er pr s-1 men der ønskes enheden h-1.
Okay, men hvorfor var det at du dividerede med de 30% i #5
Tak for hjælpen:)
Svar #18
03. april 2021 af mathon
Maksimal dosishastighed for patienten er kun 30% af strålingsintensiteten,
så denne er:
Svar #19
08. april 2021 af CecilieBebsi (Slettet)
#9Denne skal nu dæmpes ved gennemgang af beton, hvis halveringstykkelse er ca. 40 mm.
Beregning af betontykkelse:
Metoden var forkert. Der er tale om β--henfald. OG det korrekte svar var 22 cm. Ved dog stadig ikke hvilken formel/metode der skal bruges.


