Fysik
Ellære
Hej SP
Jeg har nogle spørgsmål omrking nogle småting inden for ellære, og det er:
1. Hvorfor skal spændingsfaldet måles over komponenten, mens strømstyrken skal måles i komponenten?
2. Hvordan kan resistiviteten ændre sig, hvis det er en tabelværdi? Bør den så ikke være konstant? For der findes åbenbart også en resistiviet, når temperaturen er nul grader, hvilket får resistiviteten til at ændre sig. Jeg snakker om denne formel:
3. Hvilken indflydelse har resstiviteten på resistansen?
Tak på forhånd
Svar #1
12. juni 2021 af Tippi123
4. Hvad er en resistivitet helt præcis?
5. Hvorfor er -grafen for wolfram lineær, mens den er potensiel for jern? Jeg troede, at formlen, jeg skrev deroppe, var en lineær sammenhæng
Svar #2
12. juni 2021 af ringstedLC
Svar #3
12. juni 2021 af peter lind
1) Måling af spænding er reelt en måling af strømmen gennem måleapparartet. Da man kender modstanden i måleapparatet kan det omregnes til spændingen ved hjælp af ohms lov. Strømstyrken kan måles direke
2) det er korrekt at modstanden er afhængig af temperaturen. Når der bare er angivet en værdi er det ved stuetemperatur.
3) R = ρ'L/A hvor R er modstanden, ρ er resistiviteten og A er tværsnitsarealet
Svar #4
12. juni 2021 af mathon
2)
Resistiviteten er temperaturafhængig
som angivet i din medskrevne formel:
3)
Resistivitetens indflydelse på resistansen:
Svar #5
12. juni 2021 af ringstedLC
2. Resistivitet er en tabelværdi gældende ved 20 Cº.
3. og 4.
Se https://da.wikipedia.org/wiki/Elektrisk_resistivitet#Definition_på_resistivitet
5. Vedhæft et godt billede af graferne.
Svar #6
12. juni 2021 af Tippi123
Her er et bilelde
Svar #8
12. juni 2021 af Tippi123
Et andet spørgsmål:
6. Hvad er argumentet for, at en parallelkobling har en samlet resistans, der er mindre en de enkelte resistorers resistans?
Svar #9
12. juni 2021 af MandenMedMangeHatte
#8 Der er ikke noget der hedder en samlet resistans. Der er noget der hedder en erstatningsresistans, og det er enkelt resistor der erstatter en (eller flere dele af) serie/parallelkobling af resistorer. Erstatningsresistansen af en parallelkobling vil altid minde mest om den mindste resistor i koblingen. Fx R1 = 600 og R2 = 2
Svar #10
12. juni 2021 af peter lind
Hvis to modstande er parallelkoblet og hver af dem har samme spænding over sig bliver strømmen summen af de enkelte større og ifølge ohms lov vil så erstatningsmodstanden blive mindre
Det kan du også se af sammenhænget mellem modstanden og resistiviteten. Arealerne bliver summe af de to arealer og dermed bliver modstanden mindre.
Svar #11
12. juni 2021 af ringstedLC
#6:
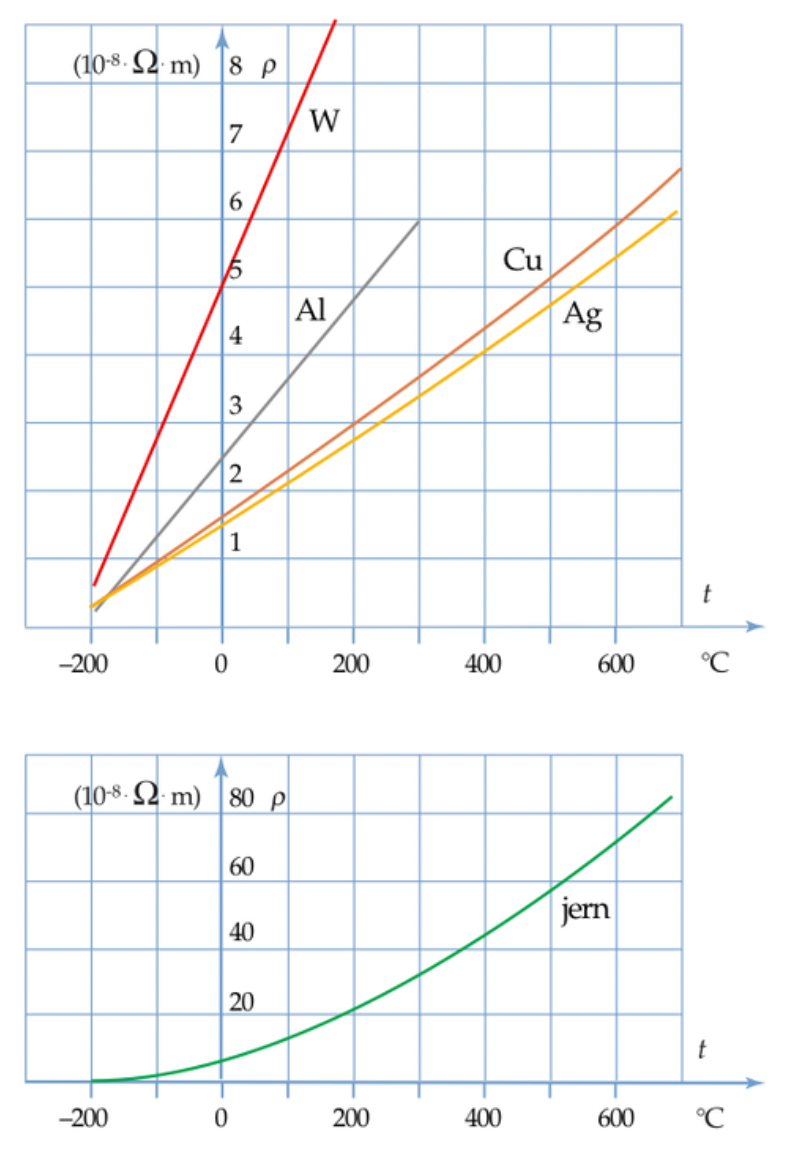
5.? α i formlen er kun den samme i et begrænset temp.-interval. Da jerns resistivitet er langt den største af de fem metaller, er grafen for jern tegnet for sig selv. Graferne for de andre krummer også ved lavere temp. end -200 ºC.
Se https://hypertextbook.com/facts/2004/BridgetRitter.shtml m.m.
Svar #12
12. juni 2021 af mathon
6. Hvad er argumentet for, at en parallelkobling har en erstatningsresistans, der er mindre en de enkelte resistorers resistans?
Svar #13
13. juni 2021 af Eksperimentalfysikeren
1: Du kan sammenligne elektrisk strøm med en vandstrøm gennem et rør. Vandet i røret drives frem af trykforskellen mellem rørets ender. Tilsvarende drives den elektriske strøm gennem en modstand af spændingsforskellen mellem enderne af modstanden.
6. Sammenlign igen med vandstrømmen. Hvis der er to rør parallelt, kan der løbe mere vand igennem ved samme trykforskel.
5. Temperaturafhængigheden er ikke lineær. For de fleste metallers vedkommende kan man betragte temperaturafhængigheden som værende lineær indenfor et vist område.
Svar #14
13. juni 2021 af Tippi123
7. Hvorfor vil strømstyrken aftage, hvis man indsætter en resistor i et kredsløb? Normalt vil der være en resistans i et kredløb, fordi kredsløbets egne elektroner frastøder hinanden, men resistoren er jo bare lavet af en dårlig leder. Hvilken indflydesle vil det have
Svar #15
13. juni 2021 af MandenMedMangeHatte
#14 Har du selv nogen ideer? Du lærer ikke noget af bare at få svarene serveret.
Svar #16
13. juni 2021 af ringstedLC
7.
Indsat i serie med kredsløbet: Ohm's lov siger, at ved konstant spænding er strømmen omvendt proportional med resistansen:
Indsat parallelt i/med kredsløbet: Erstatningsresistansen for en par.-kobling er mindre end den mindste af de koblede resistorer (igen; U er konstant):
Nu har vi næsten givet dig et helt kompendie om resistans. Du kunne godt komme med nogle flere bud på svarene efter at have læst i din bog.
Svar #17
13. juni 2021 af Eksperimentalfysikeren
#14 Frastøningen mellem elektronerne giver ikke modstand. Det er elektronernes sammenstød med de atomer, de passerer, der giver modstanden.
Skriv et svar til: Ellære
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.


