Fysik
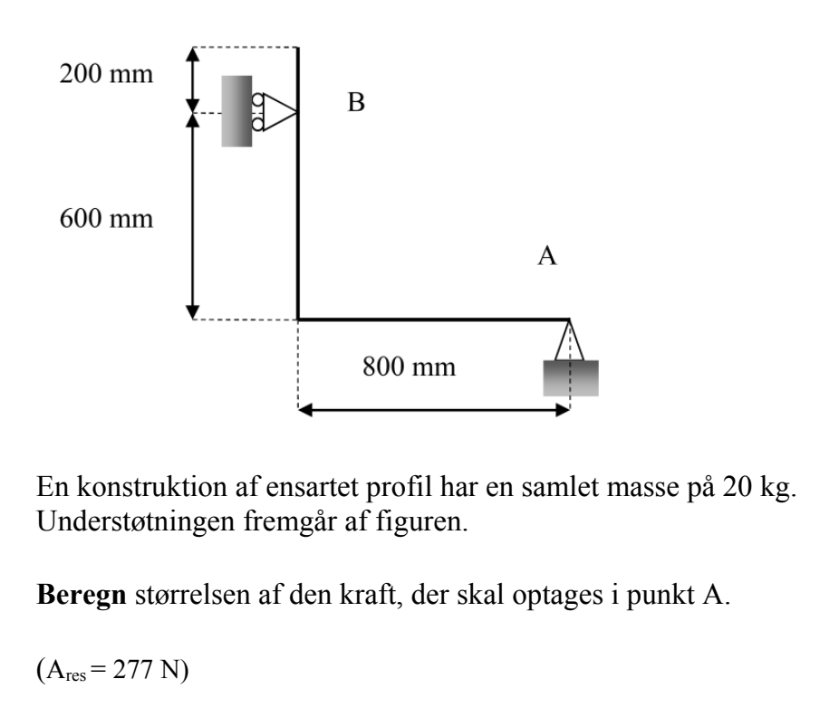
Beregn størrelse af kraften (N)
Jeg søger hjælp til denne opgave, se vedhæftet fil - facit skal give 277N
Jeg tænker at tage moment omkring punktet B men er lidt lost da bjælken er fikseret lodret.
Hvis en kunne skrive hvordan de kommer frem til facit eller et fritlegme diagram hvor alle kræfter er tegnet på ville det være en stor hjælp. Da jeg har flere opgaver som ligner, mere så jeg kommer rigtigt igang.
Tak
Svar #3
22. oktober 2021 af Idunidun (Slettet)
#0. Prøv evt at Google: static equilibrium ladder against wall.
Tak for dit svar - vil du så lade som om der står en stige mellem punkt A og B med massen 20 kg og på den måde finde reaktionen i punktet A ?
Svar #4
22. oktober 2021 af Soeffi
#3. Jeg tror, at det kan gøres på den måde, se f.eks. følgende video, du skal bare tage hensyn til at massemidtpunktet ligger et andet sted, se nedenfor:
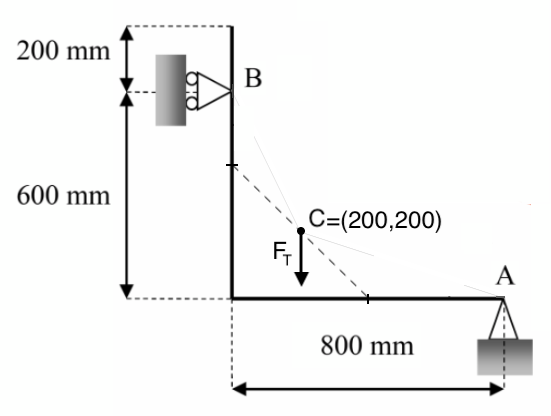
(På tegningen er samlingspunktet mellem de to vinkelben tænkt som et koordinatsystems origo.)
Svar #5
22. oktober 2021 af Idunidun (Slettet)
#3. Jeg tror, at det kan gøres på den måde, se f.eks. følgende video, du skal bare tage hensyn til at massemidtpunktet ligger et andet sted, se nedenfor:
(På tegningen er samlingspunktet mellem de to vinkelben tænkt som et koordinatsystems origo.)
Nu har jeg prøvet;
Fres,y=o =-Ft+Fn>
Ft=Fn=m*g= 20*9,82=194N
Fres,x=0=>-Fg+Fv=>
Fv=Fg
arctan(0,2/0,2)=45 grader
Ma=0=> -Fv*cos(
-Fv*cos(45)+196=0
Fv= 277N (Fv er min vektor som skubber væk fra væggen i x retningen)
Skal man så “bare” gå ud fra at den størrelse er den samme som i punktet A ? for facit er i orden :)
Svar #6
22. oktober 2021 af Idunidun (Slettet)
#4
#3. Jeg tror, at det kan gøres på den måde, se f.eks. følgende video, du skal bare tage hensyn til at massemidtpunktet ligger et andet sted, se nedenfor:
(På tegningen er samlingspunktet mellem de to vinkelben tænkt som et koordinatsystems origo.)
Nu har jeg prøvet;
Fres,y=o =-Ft+Fn>
Ft=Fn=m*g= 20*9,82=194N
Fres,x=0=>-Fg+Fv=>
Fv=Fg
arctan(0,2/0,2)=45 grader
Ma=0=> -Fv*cos(
-Fv*cos(45)+196=0
Fv= 277N (Fv er min vektor som skubber væk fra væggen i x retningen)
Skal man så “bare” gå ud fra at Fv=Fg og det er den størrelse som er i punktet A ? for facit er i orden :)
Svar #7
22. oktober 2021 af Soeffi
#4. A påvirkes af en lodret kraft, FA,lod , der er lig med tyngdekraften fra bjælken og vandret af en kraft, FA,van , der er lig med normalkraften på bjælken i B. Denne kan findes ud fra kraftmomentet omkring A:
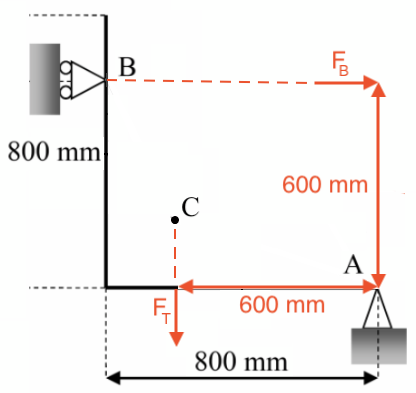
Den samlede kraft på A fra bjælken findes ud fra FA,lod og FA,van ved hjælp af Pythagoras: FA,res = √[(FA,lod)2 + (FA,van)2]. Det fremgår af tegningen, at FT = FB og dermed af FA,lod = FA,van. Dermed er FA,res = √2 · FT = √2 · 20 · 9,82 N = 278 N.
Svar #8
22. oktober 2021 af Soeffi
#7...Det fremgår af tegningen, at FT = FB, fordi armen er den samme (600 mm). Dette giver at FA,lod = FA,van. Dermed er FA,res = √2 · FT = √2 · 20 · 9,82 N = 278 N.
Svar #9
22. oktober 2021 af Idunidun (Slettet)
#7...Det fremgår af tegningen, at FT = FB, fordi armen er den samme (600 mm). Dette giver at FA,lod = FA,van. Dermed er FA,res = v2 · FT = v2 · 20 · 9,82 N = 278 N.
Ja okay, kan godt se at det er en ligesidet trekant når du tegner det sådan. Men var aldrig kommet frem til at Ftyn *V2=Fa,res. Men tak alligevel :)
Så går ud fra det jeg har gjort er skrup forkert ?
Svar #10
22. oktober 2021 af Soeffi
#9...Så går ud fra det jeg har gjort er skrup forkert ?
Jeg er ikke sikker. Skal jeg være ærlig, så var jeg selv ude i nogle lange beregninger før, jeg så videoen!
Svar #11
22. oktober 2021 af Idunidun (Slettet)
#9...Så går ud fra det jeg har gjort er skrup forkert ?
Jeg er ikke sikker. Skal jeg være ærlig, så var jeg selv ude i nogle lange beregninger før, jeg så videoen!
Nej den er ikke lige til den opgave. Men lige et sidste spørgsmål, du skriver at Ft=Fb da armen er lige lange (600mm)
Så går jeg ud fra at du tager armen ind til tyngdepunktet og ikke helt ud til punktet B ikke, for ellers ville den vel være (800mm)
Svar #12
22. oktober 2021 af Soeffi
#11...Så går jeg ud fra at du tager armen ind til tyngdepunktet og ikke helt ud til punktet B ikke, for ellers ville den vel være (800mm)
Armene fremgår af tegningen:

Rotationen antages at foregå omkring A (det er valgfrit). Hvor virker kræfterne? Svar: I B (vandret kraft) og lodret under C (lodret kraft). Armene er vinkelrette på kræfterne som vist. En kraft og dens arm kan parallel-forskydes for anskuelighedens skyld.
Svar #13
22. oktober 2021 af Idunidun (Slettet)
#11...Så går jeg ud fra at du tager armen ind til tyngdepunktet og ikke helt ud til punktet B ikke, for ellers ville den vel være (800mm)
Armene fremgår af tegningen:
Rotationen antages at foregå omkring A (det er valgfrit). Hvor virker kræfterne? Svar: I B (vandret kraft) og lodret under C (lodret kraft). Armene er vinkelrette på kræfterne som vist.
Så jeg med, det selvfølgelig fra når man tager moment omkring A at man har samme arm i (den ligesidet trekant så og sige). Nogle gange stirrer man sig lige blind. Tak :)
Svar #14
22. oktober 2021 af Soeffi
#12. Angående valg af omdrejningspunkt. Antag at man vælger massemidtpunktet C i stedet for A.
Nedenunder er følgende vist:
1: Kræfterne i systemet:
A: En vandret normalkraft (ukendt) og en lodret normalkraft (lig med tyngdekraften).
B: En vandret normalkraft (ukendt og lig med den vandrette kraft i A).
C: Tyngdekraften i massemidtpunktet.
2: Når man vælger C som omdrejningspunkt, så ses bort fra den kraft der virker i punktet. Tilbage er de tre
kræfter i A og B. Man konstruerer en vinkelret arm til kraften i B som vist.
3. På samme måde konstrueres vinkelrette arme til kræfterne i A. Det ses, at de vandrette kræfter i
henholdsvis A og B har samme omdrejningsretning og derfor skal lægges sammen. Da kræfterne er ens,
kan man nøjes med at lægge armenes længder sammen og gange summen af disse med kraften i B.
Armen fra C til den lodrette kraft i A har længden 600 mm. Summen af armene til de vandrette kræfter giver
også 600 mm, så man får samme resultat, som da man brugte A som omdrejningspunkt.
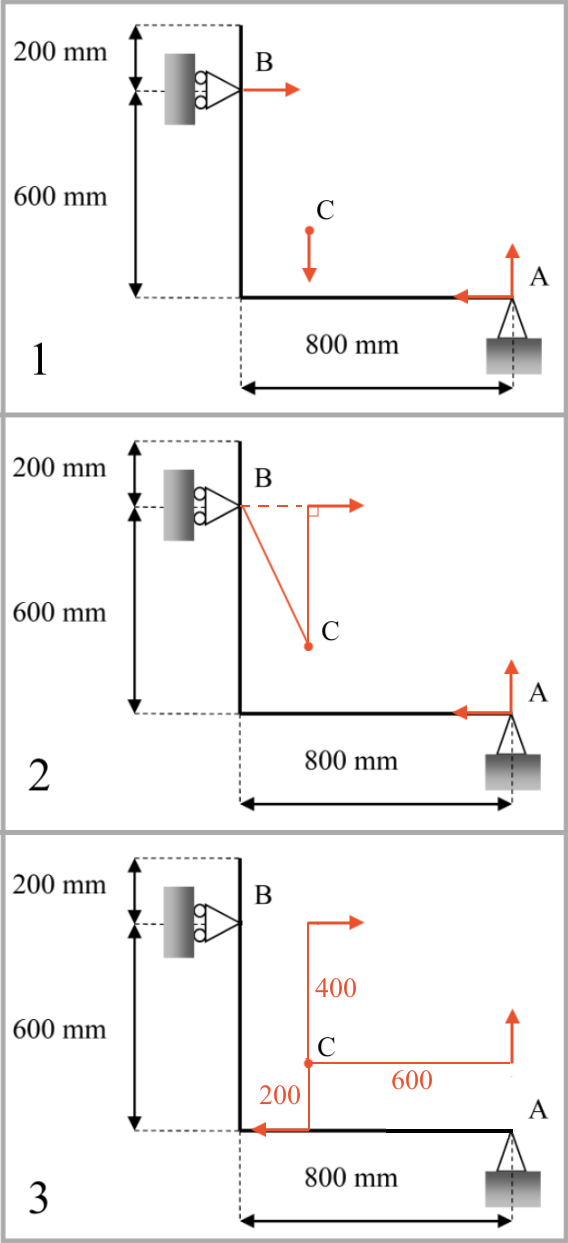
Som det ses er det bedst at vælge det punkt, som der er flest kræfter i, som omdrejningspunkt, da man ser bort fra disse kræfter i beregningerne. Det vil her sige punktet A.
Skriv et svar til: Beregn størrelse af kraften (N)
Du skal være logget ind, for at skrive et svar til dette spørgsmål. Klik her for at logge ind.
Har du ikke en bruger på Studieportalen.dk?
Klik her for at oprette en bruger.